Based on “Progress Toward an Open-Source Drilling Community: Contributing and Curating Models,” IADC/SPE-208794-MS, SPE/IADC International Drilling Conference and Exhibition, Galveston, Tex., Mar. 8-10, 2022.
The high cost of drilling has driven industry to incorporate as much modeling as possible to minimize risk and rig time. Drilling models require a combination of physics-based fundamentals with simplified assumptions for broad-based applicability. Field-based data qualifies and tunes the models to provide accurate forward-looking simulations of drilling operations for feasibility studies.
Drillers have a wide range of models to choose from, and the industry needs validated open-source models for drilling studies or for benchmarking proprietary models. The Open-Source Drilling Community (OSDC) shares such models with industry and academia. Access to original code source from existing qualified work saves time on coding for new models, freeing it up for modelling advances and allowing others to inspect the work based on the larger drilling community’s experiences. Commercial models, by contrast, are usually proprietary and code is unavailable for review. Comparing open-source models to commercial results yields insights into the proprietary code, and differences between modelling results can lead to further insights and upgrades to one or both models.
Open-source drilling charter
The Drilling Systems Automation Technical Section Open-Source Subcommittee was chartered under the SPE Drilling Systems Automation Technical Section in 2019. This subcommittee oversees and fosters the OSDC. OSDC follows the specifications of the Open-Source Initiative (OSI), created in the late 1990s, that parties will not be restricted in selling or giving away open-source software and that open-source software must include source code and “must allow distribution in source-code as well as compiled form.” Persons who are not members of SPE may attend, participate, access, use, and submit models, data, and comments to OSDC sites, but cannot hold officer positions within the subcommittee.
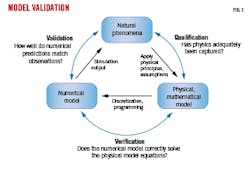
Models contributed to OSDC are either physical models, which are mathematical representations of drilling phenomena, or numerical models approximating mathematical solutions via algorithms using finite-difference or finite-element discretization procedures. Numerical models are used for computational efficiency. Qualification of physical models determines if a model accurately captures details of the phenomena of interest. Verification ensures that a numerical model accurately represents a physical model. Fig. 1 shows the process of verifying and validating both types of models, both against observed data and each other.
Verification of numerical model fidelity includes:
- Analytical benchmarks comparing numerical model results to governing equations of physical models.
- Numerical benchmarks comparing numerical model results against predictions from previously published solutions obtained from other numerical models.
- Stability analysis to evaluate and quantify the numerical model stability under implementation of time-integration procedures and wellbore-drillstring contact algorithms.
- Grid and mesh convergence based on a function of mesh size.
- Validation of numerical model predictions and field data matches.
Model validation is an iterative process which can lead to model refinements. Important elements of model validation include non-trivial field test cases, metric matching, hierarchy of validation assessments at the unit, component, subsystem, and complete system levels, and uncertainty quantification.
Coding best practices
Submitted models to OSDC are expected to follow coding best practices including comments, variable definitions, formatting, and documentation. Avoiding generic names for variables is recommend. Use concrete names for functions and use clean formatting. The two most common languages of the initial submitted models are Matlab and Python.
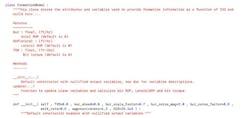
Documentation tools which automate generation of code-line function descriptors, code functions, classes, etc. are encouraged but not required for submitted code. Documentation tools taking advantage of reStructuredText (reST) syntax are recommended. Fig. 2 shows an example of well-formatted code.
Modular code is recommended to provide interoperability between models and saves time by maintaining code bases of different groups of functions, classes, and modules. These groups serve as building blocks for model and simulator development regardless of end-use function. Models constructed from individual elements can be integrated into larger hierarchical models.
Discrepancies between code written in different languages (Java, Python, etc.) are addressed by the micro-service architecture. It consists of a suite of small services that are independently deployable and scalable, are independent of each other, have their own local storage, and can be developed in various programming languages. They also can be managed by different teams. The interface to the service is standardized and typically adheres to generic application program interface API:CRUD (create, read, update, and delete) commands.
Packaging an algorithm or method into a microservice requires significant programming effort. But once done, the containerized microservice can run on various software platforms and its functionalities can be accessed from any software platform and programming environment. Packaged microservices can provide multiple solutions to the same problem and offer an opportunity to determine the best approach to a given problem and quantify uncertainties in modelling approaches.
Model library
The model library currently contains a simple torsional model, a coupled axial-torsional model, a mechanics and dynamic simulator, and a model for horizontal directional drilling (HDD). It also has models to integrate downhole mud-motors with current drilling simulators and calibrate yield power law rheological behavior from a rheogram.
- Simple torsional model. This model assumes that rotational dynamics dominate and distributes friction along the wellbore. Dynamics are described by a damped wave equation with a frictional term. The model has been validated with field data and has been documented in several publications. Fig. 3 shows the key validation of the model. The model is limited to the assumption that torsional dynamics are dominant. The drillstring is modeled off bottom, and axial motion and bit-rock interaction are not considered. The model does not match vertical well data accurately where there is minimal normal force and friction in the system.
- Coupled axial-torsional model. A time-based transient modeling tool with governing drill-string dynamics models the drillstring while tripping and drilling. The tool predicts severity of vibrational dysfunctions on drilling performance. It uses a coupled 2D axial-torsional system and is available as a lumped-parameter study in MATLAB, Python, and Simulink programming.
The drillstring is segregated into drill pipe, heavyweight pipe, collar, and BHA elements. A combined Stribeck and viscous friction model accounts for borehole frictional forces of pipe and BHA. The net frictional force depends on gravity, string buoy weight, and well inclination. Drillstring mass, inertia, and axial and torsional stiffness is included, but bending stiffness is currently neglected. The bit-rock interaction is governed by a depth-of-cut based algorithm tracking the bit interaction with the bottom of the hole.
- Downhole mud-motor integration. Motor performance is described by the relationship between pressure drop and torque, and flow and RPM. Flow rate through the drilling system is translated into output rotary speed, and differential pressure across the motor is a function of downhole reaction torque. Modelling includes reactions of the system from slide to rotate, pipe rocking, and other transient events. Frictional losses from flow in the drillstring to the motor, delay from fluid compressibility, and string stretch from pressure variations along the length of the drillstring are not considered in the current model.
- Drilling simulator. Current work involves integrating a surface autodriller controller on top of a drilling simulator to predict stability of different control systems with varying downhole conditions. Efforts are also underway to introduce new modules such as dynamic hydraulics and hydraulic string-stretch effects into the model to better represent transient events such as bit stalling and mud-motor stalling.
- Calibration of yield power law. High-performance drilling muds are not accurately modelled as Newtonian or Bingham Plastic fluids. The Herschel-Bulkley yield power law model provides more accurate results. The calibration of this model is usually performed using rheometer measurements, typically from a Couette geometry. A quadratic fit is required to fit the model to the rheogram. For small shear stresses, inaccurate linear fitting of consistency and flow -behavior indices can occur. The calibration model uses the Newton-Raphson method to solve the linear equation. It is less sensitive to measurement errors for small shear stresses.
Two calibration methods have been implemented in a C# micro-service: a data model to describe a rheogram and another data model to describe yield power law rheological behavior. The yield power law class has two calibration methods and, after fitting, Herschel-Bulkley parameters are updated, as is the variance between model and test results.
Mechanics, dynamic simulator
A new validated proprietary model calculates downhole mechanics and dynamics based on a 3D nonlinear finite element formulation. The model includes:
- Fully coupled flexibility of the drillstring (axial-lateral and lateral-torsional displacement dependencies).
- Geometric nonlinearity (large-displacement, small strain).
- Automatic determination of frictional wellbore contact points with arbitrary radial clearance.
- 3D wellbore profiles, with variable wellbore diameters.
- Added fluid mass and damping effects from the hydrodynamic forces generated between the moving drillstring and surrounding fluid.
- Complex tool geometry (including steerable mud motors, rotary steerable systems, and eccentric stabilizers).
- Shear-beam deformations, lateral rotary inertias, and gyroscopic effects.
Simplifications to the system can examine nonlinear quasistatic deflection of the drillstring and BHA in an arbitrary 3D wellbore, linearized dynamics of the system, or fully nonlinear dynamic behavior with time integration.
The full model is not available in open source, but the simplified version of the code is available for straight wellbores only with constant wellbore OD. There are no provisions for buckling or dynamic calculations. Additionally, the graphic user interfaces and advanced plotting features have been removed. The simplified model is available to support the open-source project as a reference point to build upon.
HDD
The HDD simulator trains new operators by modelling the following drilling parameters from a predefined drill bit crossover, orientation sub, bent sub, and navigation probe configuration to approximate the physics of drilling:
- Bit-probe orientation.
- Rate of penetration.
- Build rate.
- Drillstring dynamics with torsional deformation.
- Debris generation and circulation.
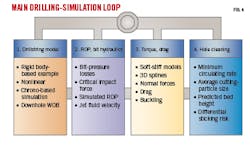
The simulator is written in C++ using open-source code developed in other industries and academic disciplines. Fig. 4 lists some of the modules included in the main drilling simulation loop. Modules 2 and 3 have been converted to Python and committed to the repository.
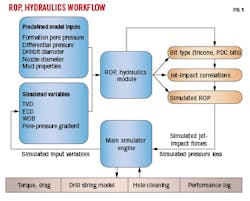
The simulator works with the modules simultaneously and the modules use static and dynamic parameters as input to simulate bit impact forces, erosion velocities, frictional contact forces, etc. The ROP and bit hydraulics module, for example, takes simulated jet-impact forces derived from hole geometry, drillstring diameters, and bit-nozzle configuration to estimate ROP based on rock strength and pore pressure. Bit hydraulic values from this module are transferred to the hole cleaning module to compute lift and drag coefficients and cutting bed heights. Fig. 5 shows the workflow for the ROP and hydraulics simulator and its connections to the other modules.
OSDC status
Multiple models have been submitted to OSDC under the Massachusetts Institute of Technology open-source license, and the initial web and GitHub site are online and open. Submitted models will be reviewed by the steering committee which will provide feedback to model creators. Requirements for validation and verification data will be defined and continuously refined. The committee will also suggest areas for further research. It is expected that models will be continuously upgraded or replaced. Accurate documentation is key to identifying changes throughout a model’s development period. Interested parties can join the effort by going to the OSDC website (https://github.com/Open-Source-Drilling-Community/) and adding contact information to the mailing list under the Contribute tab. There is no cost to join or use models from the community.
About the Author
Alex Procyk
Upstream Editor
Alex Procyk is Upstream Editor at Oil & Gas Journal. He has also served as a principal technical professional at Halliburton and as a completion engineer at ConocoPhillips. He holds a BS in chemistry (1987) from Kent State University and a PhD in chemistry (1992) from Carnegie Mellon University. He is a member of the Society of Petroleum Engineers (SPE).