New PVT models describe Rmelan crude

An ANN model offers the most accurate and reliable prediction of bubble-point pressure for Rmelan crude oils. For practical field applications, an empirical correlation can serve for preliminary estimates but will not provide the most accurate estimates for reservoir studies, production forecasting, and reserves calculation.

Dec. 9, 2025

21 min read

Key Highlights

Rmelan field in northeastern Syria lacks PVT sampling and analysis due to war damage.
The study developed predictive PVT models for Rmelan crude oil using empirical correlations and artificial neural networks.
Empirical correlations for bubble point pressure were suitable for preliminary estimates but not for detailed reservoir studies.
A neural network model produced the most accurate and reliable for predictor for bubble point pressure.

Correlation 1 parametric sensitivity (Fig. 1)

Youssef Ibrahim
Rojava University
Qamishli, Syria

Sayed Gomaa
Tarek M. Aboul-Fotouh
Abuzeid Ali
Al-Azhar University
Cairo, Egypt

Rmelan field lies in northeastern Syria and is one of the largest oil fields in the Kurdish region. War damage has prevented Rmelan Oil Co. from extracting and preserving bottom hole oil samples for PVT analysis. Predictive PVT methods aid estimates of original oil in place and reserve calculations, but there are no correlations to predict bubble-point pressure (Pb) for Rmelan crude oil. The lack of PVT modeling, therefore, limits further exploration of the field.

To address this shortcoming, researchers at Rojava and Al-Azhar universities constructed four predictive PVT models based on Rmelan data. Two of the models used empirical correlations, and two used artificial neural networks (ANN). The models were tested against a Rmelan PVT database of 50 samples.

Rmelan field

Rmelan field lies in northeastern Syria 70 km east of Qamilshi and 30 km southwest of Al-Malikiyah-Derik. Discovered in 1958, development has made it one of the largest oil fields in the Kurdish region. The field contains an estimated 315 billion bbl of undiscovered and 69 billion bbl discovered reserves.

The war has restricted Rmelan Oil Co.’s ability to perform PVT analyses by damaging the only device in country which extracts and preserves bottom-hole crude oil samples. The lack of PVT data limits further reserve estimates and production analysis for the field.

Repairing and returning the equipment to service is unlikely, necessitating the use of alternative methods to accurately determine reservoir fluid properties. To address this situation, the current study developed new empirical and ANN-based PVT correlations for Rmelan crude oil.

Empirical correlations

Given that Pb is one of the most important PVT fluid properties, two empirical correlations focused on achieving accurate Pb predictions based on existing Rmelan data. One sample each from 50 Rmelan oil reservoirs comprise the dataset used in developing the correlations (Table 1). The data represent bubble-point pressure as a function of reservoir temperature, solution gas-oil ratio (GOR), API gravity (°API), and gas specific gravity. Collected data cover 163.57–1,472.11 psi Pb, 149–186.8 ℉. reservoir temperature, 73–420.28 scf/stb solution GOR, 26.42–43.19 °API oil gravity, and 1.05–3.60 gas specific-gravity ranges.

Empirical Correlation 1 predicts Pb as a function of reservoir temperature, solution GOR, °API, and gas-specific gravity. Equation 1 describes the correlation.

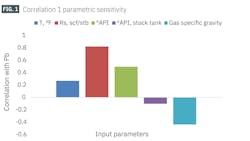
Fig. 1 shows the effects of the input parameters on Pb from the correlation. Pb is directly proportional to reservoir temperature, solution GOR, and °API calculated at reservoir conditions. Conversely, Pb is inversely proportional to gas-specific gravity and °API at the stock tank. Correlation coefficients (R²) between these parameters and Pb include R² = 26.7% for reservoir temperature, R² = 82% for solution GOR, R² = 50% for °API, and R² = -43.78% for gas specific gravity. The correlation of °API at stock tank conditions to Pb is neglected due to its small effect on the bubble point pressure.

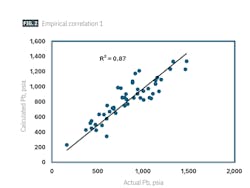
Fig. 2 shows calculated versus actual Pb. There is a high correlation between the actual and calculated Pb with R² = 0.87.

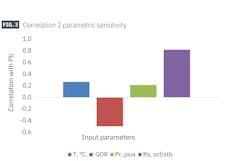
Empirical Correlation 2 was developed to predict Pb as a function of reservoir pressure, reservoir temperature, solution GOR, and oil-specific gravity. Fig. 3 shows the effect of the input parameters on Pb for this correlation. Pb is directly proportional to reservoir temperature, reservoir pressure, and solution GOR and inversely proportional to oil specific gravity. Correlations include R² = 26.7% for reservoir temperature, R² = 21.28% for reservoir pressure, R² = 82% for solution GOR, and R² = -49.647% for oil specific gravity.

Correlation 2 parametric sensitivity (Fig. 3)

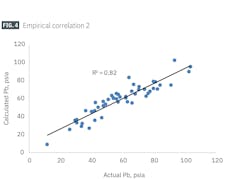
Fig. 4 shows calculated versus actual Pb. There is a high correlation between the actual and calculated Pb with R² = 0.82.

ANN correlations

Before building ANN models, reservoir sample data were divided into two sets. The first set trained the model and included 35 out of the 50 datasets, while 15 sets validated and tested the performance of the model. To build the ANN model, all data were normalized between −1 and 1.

ANN Model 1 estimates Pb as a function of reservoir temperature, solution GOR, °API at reservoir conditions, and gas-specific gravity at reservoir conditions. ANN Model 2 estimates bubble point pressure as a function of reservoir pressure, reservoir temperature, oil-specific gravity at reservoir conditions, and solution GOR.

The models contain three layers: the input layer, which has four neurons for inputs, a hidden layer, which contains eight neurons, and an output layer, which has one neuron to predict Pb. A Levenberg-Marquardt technique was selected as a training algorithm with pure-linear as the output function. Equations 3-8 derive the first ANN model and Equations 9-10 derive the second ANN model.

ANN Model 1 tan-sigmoid transfer function accuracy (Table 2)

ANN Model 1 log-sigmoid transfer function accuracy (Table 3)

Table 2 shows the ANN Model 1 Tan-sigmoid transfer function correlation results in terms of R², standard deviation (SD), and absolute error (AE) for hidden neurons 5-13. The tenth neuron had the highest R² coefficient and the lowest AE.

Table 3 shows the results of the logistic-sigmoid transfer function for these neurons. Based on comparison with the Tan-sigmoid function, the optimum transfer function is Log-sigmoid with 11 neurons. with R² = 0.88 and AE = .082 %. The characteristics of the proposed model are presented in Table 4.

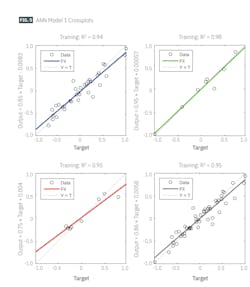
Regression plots for the Pb model show the relation between network outputs and targets for training, validation, testing, and all data points (Fig. 5). All datasets show good fit with R² = 0.88 for the test dataset.

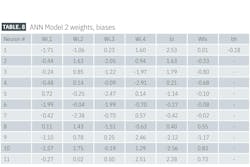
Table 6 shows the ANN Model 2 Tan-sigmoid transfer function correlation results in terms of R², SD, and AE for hidden neurons 5-13. Like the first ANN model, the tenth neuron had the highest R² coefficient and the lowest RMSE.

ANN Model 2 tan-sigmoid transfer function accuracy (Table 6)

Table 7 lists the logistic-sigmoid transfer function for these neurons. Based on comparison with the Tan-sigmoid function, the optimum transfer function is Log-sigmoid with 11 neurons, with R² = 0.94 and AE = .057. The characteristics of the proposed model are the same as in Table 4.

ANN Model 1 log-sigmoid transfer function accuracy (Table 7)

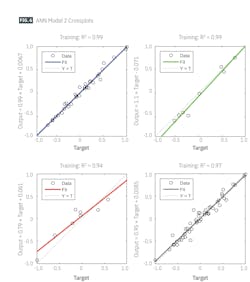
Regression plots for the Pb model show the relation between network outputs and targets for training, validation, testing, and all data points (Fig. 6). All datasets show good fit with R² = 0.94 for the test dataset. This study showed that the developed ANN models match Rmelan crude oil properties better than other published correlations.

Discussion

The empirical correlations achieved satisfactory performance, particularly Correlation 1, which yielded an R² value of 0.87. The correlation provides a good fit to the calibration data. Empirical correlations, however, are typically constrained by the specific data ranges from which they are derived. Their predictive capability may deteriorate when applied beyond those ranges or under strongly nonlinear reservoir conditions.

By contrast, the ANN models demonstrated superior flexibility and adaptability to the complex, nonlinear relationships among the reservoir parameters. Both ANN models reduced the prediction error compared with empirical formulations. ANN Model 1, which used temperature, solution gas–oil ratio, °API, and gas specific gravity as inputs, achieved R² = 0.88 with an average error of 0.082. ANN Model 2 incorporated reservoir pressure as an additional input and improved the prediction accuracy significantly, reaching R² = 0.94 and AE = 0.057. The use of the Levenberg–Marquardt training algorithm and a log-sigmoid transfer function contributed to the efficient convergence and stable network performance.

Although Correlation 1 displayed a high R² value numerically, it’s purely statistical nature limits its general use. The ANN models, particularly Model 2, provided more physically consistent and data-driven representations of the PVT behavior of Rmelan crude oils. The inclusion of reservoir pressure in Model 2 enhanced the network’s ability to capture dynamic effects that influence gas liberation and saturation conditions.

Model selection

The comparative evaluation, therefore, confirms that ANN Model 2 offers the most accurate and reliable prediction of bubble-point pressure for Rmelan crude oils. For practical field applications, Correlation 1 can serve as a convenient tool for preliminary estimates when computational resources are limited. For accurate reservoir studies such as forecasting and reserves calculation, the ANN-based models provide higher accuracy.

Bibliography

Ahmed, T., “Reservoir engineering handbook,” Gulf Professional Publishing, 2018.

Heidarian, M., Karimnezhad, M., Mahin Schaffie, M., and Ranjbar, M., "An Intelligent Model for Estimating Bubble Point Oil Formation Volume Factor,” Petroleum and Coal, Vol. 58, No. 2, 2016, pp. 240-246.

Authors

Youssef Ibrahim ([email protected]) is a professor of petroleum reservoir engineering at Rojava University, Syria. Youssef holds an MS (2023) in petroleum engineering from Rojava University.

Sayed Gomaa ([email protected]) is a professor of petroleum reservoir engineering at Al-Azhar University, Cairo, Egypt. Sayed holds a Ph.D. (2010) from the Azerbaijan State Oil Academy.

Tarek M. Aboul-Fotouh ([email protected]) is a professor of petroleum refining engineering at Al-Azhar University. Aboul-Fotouh holds a Ph.D. (2010) in chemical engineering and fuel technology from Azerbaijan State Oil and Industry University in Baku, Azerbaijan. He is a member of the Society of Petroleum Engineers (SPE).

Abuzeid Ali ([email protected]) is a professor of petroleum production engineering at Al-Azhar University, Cairo, Egypt. Abuzeid holds a Ph.D. (1998) from Al Azhar University.