Hubbert’s model: uses, meanings, and limits-1
It is well known that M. K. Hubbert successfully predicted the timing of peak US oil production. Since then, Hubbert’s model has been used extensively to predict peak oil production elsewhere, and the derived bell-shaped curve to describe production has appeared in many publications. However, forecasts of world and regional peak oil and natural gas production using this methodology have usually failed, leading to the implicit belief that such predictions will always fail and that we need not worry about finite resources.
The questions that must be asked are why the model succeeded for the US and what this can teach us about petroleum production modeling. A careful examination of Hubbert’s approach indicates that the most important reasons for his success in the US were stable markets, the high growth rate of demand, ready availability of low-cost imports, and a reasonable estimate of easily extractable reserves. This analysis also shows that his model cannot predict ultimate oil reserves and that it should be considered an econometric model.
Building on Hubbert’s vital insight, that cheap fossil fuel reserves are knowable and finite, one can state that for peak world oil production, political constraints should be much more important than resource constraints.
Nonrenewable resources
While it is nominally understood that petroleum and natural gas are not renewable resources, modern industrial society has been operating quite successfully as if they were. Economic growth, based on widely available, extremely profitable, and easily affordable fossil fuels, has been impressive in the developed world.
Now those nations that have not been part of this process, such as China and India, with about 2.2 billion people, are beginning to demand their share of these resources. The importance of understanding resource limitations has therefore grown proportionally.
Almost from the beginning of the US petroleum industry in 1859, there was speculation over when the US might run out of oil. Such dire predictions had invariably been proved wrong as new frontiers were opened up and new discoveries made. Perhaps the first of a continuous stream of warnings was by a Pennsylvania geologist, who in 1874 stated that the US would run out of oil by 1878.1 New fields in Indiana almost immediately voided this judgment, but this scenario was repeated time and time again in the future.
By the late 1920s, the central problems were not shortages but oversupply and collapsing prices after the discovery of the gigantic East Texas field and the start of the Great Depression. Between 1929 and 1932, US demand dropped by 22%, and prices dropped from over $1.15/bbl (1930 dollars) to 10¢/bbl.2 Only the joint action of federal and state governments to create and enforce a system to proration (production-ration) supplies to meet but not exceed demand restored order to the industry. Coincidently, this system forced prices to return to acceptable levels, which were a factor of 25 above production costs of the most efficient producers.
US petroleum supplies from the seemingly limitless fields in Texas were a major factor in the Allied victory in World War II. By the 1950s, with the US economy and oil consumption booming, the notion that the US might not be able to satisfy petroleum demand internally seemed far-fetched, and when US production finally did peak in 1970, this came as a surprise to those few people outside the industry who monitored petroleum production. Even today, after oil production has peaked or reached a plateau in the great majority of producing regions3 around the world (such as the US, North Sea, and China), those who maintain that world oil resources will not be able to satisfy demand far into the future are ridiculed,4 although some in the industry have begun to acknowledge that demand could exceed supply in the near future.5
It is clear that the concept of limits to growth is difficult for most people to accept. Many decades of increased economic activity and spectacular progress in all areas of science and technology have created the impression that such a state of affairs is a permanent component of Western civilization. Yet limitations are also a fundamental part of the natural order, and sooner or later we must face up to this. In particular, fossil fuel resources, an essential input into any modern economic system, are finite. Understanding this measurably and mathematically, not just qualitatively, is crucial if society is to cope with depletion of these resources. Examining the reasons for the success of the best known depletion model, that of Hubbert, in dealing with this problem allows one to determine if it is applicable to current conditions-and, if not, what might be appropriate.
Logistic curves
Hubbert6 7 was the first to treat the issue of depletion quantitatively and observed that cumulative production of an exhaustible resource as a function of time (t, years) often (but not always) followed a logistic growth curve, given by:
| Q(t) = Qmax /(1 + a exp bt) | (1) |
where Qmax is the total resource available (ultimate recovery of crude oil), Q(t) the cumulative production, and a and b are constants. Production (the first derivative of Equation 1) begins slowly, then grows exponentially, reaches a maximum, and then declines. Characteristics of this equation are that it is symmetric about the point of maximum annual production and that the rate of rise and decline of annual production are identical.
Maximum annual production is given by:
| Pmax = Qmax |b|/ 4 | (2) |
the year of maximum annual production by:
| tmax = (1/b)1n(1/a) | (3) |
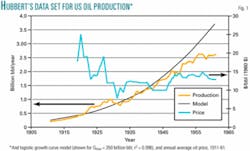
As discussed in his 1962 monograph, Hubbert plotted US crude oil production data from 1911 to 1961 on semilog paper and determined the parameters a, b, and Qmax in Equation 1 that best fit, according to his judgment, these data; at the time, this methodology was perfectly acceptable. He found Qmax=170 billion bbl, a=46.8, and b=-0.687 (Table 1), with a base year of 1910.5.
This type of equation can be fitted to these data through use of parameters with many different values, and with modern techniques goodness of fit can be determined quantitatively. Hubbert’s data set (Fig. 1) has been regenerated.8 9 For 150 billion bbl≤Qmax≤600 billion bbl, the values of a and b and goodness of fit (r2) have been determined with the Trendline option in Excel. Results are listed in Table 1. Note that Hubbert’s fit is quite reasonable; for his Qmax, the parameters a and b are quite close to those obtained from the fitting routine with an r2 of 0.9987.
However, over the range 150 billion bbl≤Qmax≤600 billion bbl (Table 1), the goodness of fit differs only in the third decimal place, with 0.9991≥r2≥0.9946; the model result for Qmax=350 billion bbl, a factor of two greater than Hubbert’s choice, is shown in Fig. 1. This should be expected with an exponential equation with three free parameters; based on goodness of fit, there is no reason to choose any one of these numbers for Qmax. This reflects a fundamental reality: Past production and consumption cannot predict the total amount of oil that is in the ground. Hubbert’s assertion that his curve-fitting to past production could reveal ultimate oil reserves is not justified.
The best fit to the data is given by Qmax=150 billion bbl (r2=0.9991), yielding a peak year of 1964, only a few years from the date of Hubbert’s publication (1962). At that time, US oil production was 7.1 million b/d, but shut-in capacity (as Hubbert noted) was 3.6 million b/d, and, as will be discussed later, many US producers wanted to increase production as rapidly as possible. Hubbert defined shut-in capacity as the difference between maximum well output, regardless of availability of pipeline capacity or storage facilities, and allowed production. There was no indication that there would be a peak in production due to resource constraints in the immediate future; thus, the lowest estimate of ultimate oil reserves could be rejected.
This emphasizes the importance of independent estimates of reserves. To be relevant, they must be based on assumptions of certain minimum levels of profitability and current technology or reasonable extensions thereof. The further into the future one attempts to see, the higher the risk, since at a minimum technology, if not market price, will advance and enable more oil to be recovered at a given price-or so it seemed in 1961.
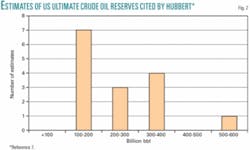
Hubbert estimated ultimate oil reserves in two other ways. He reviewed 14 independent reserves estimates made between 1956 and 1961 (Fig. 2). Seven estimates were between 145 billion bbl and 200 billion bbl, three between 200 billion bbl and 300 billion bbl, and the other four between 300 billion bbl and 600 billion bbl. The methodology used to obtain these different estimates is discussed in only one case. Some estimates were made by teams of oil company geologists, while others may have been quite simplistic approximations. At this time, such efforts were much more art than science and followed more from educated guesswork than rigorous analysis.
Hubbert also estimated Qmax using logistic growth curves as applied to large and small field discovery. He admitted that this approach, while it agreed with other results, was “valid as to order of magnitude” accuracy and believed that the curve fit to consumption and production was much more reliable.
His choice for Qmax (170 billion bbl) was in agreement with the great majority of reputable experts at the time; he also noted that Qmax might be as large as 225 billion bbl, and so his estimate for the year of peak production fell between 1967 and 1973 (Table 1). The forecast was audacious, given that the amount of US spare capacity relative to production during this period was enormous. To put this into perspective, in 2004 world oil production was 80 million b/d; spare capacity would need to be 44 million b/d to be equivalent to US conditions in 1962. To predict that US production would peak in less than 10 years given this much spare capacity seemed at the very least completely unrealistic to most people.
Hubbert had several factors in his favor when he made his prediction. He had access to reliable reserves and production data, which the Texas Railroad Commission and similar organizations in other states needed to align US production with demand in their efforts to maintain reliable supplies, avoid waste, and keep prices far above production costs. This information was collected by US government agencies as well as by the American Petroleum Institute and was available to the public. These data showed that discovery rates for large fields had declined substantially, from about five per year in 1945-50 to about one per year in 1950-60, while production and consumption increased rapidly. To supply ever-increasing consumption from a greater and greater number of smaller and smaller fields had a strong practical limit.
Most important of all, the rate of increase of demand was high. In the 1950s US demand for petroleum increased by 4.7%/year (doubling time: 15 years) and in the 1960s by about 3.9%/year (doubling time: 18 years). This put the entire system under great strain since not only did the number of wells need to increase, but also all the infrastructure associated with moving oil to market had to expand. Lower rates of demand growth allow for more improvements in technology, changes in market rules, and political upheavals, any one of which can render models and the forecasts based on them invalid.
In 1972, shortly after US production peaked at about 9.4 million b/d, demand-taken to be petroleum products supplied, including crude oil production, natural gas liquids, processing gains, and net imports-increased by 7.1%, or 1.1 million b/d, to 16.4 million b/d. US production had not kept pace so that by 1972 imports supplied about 27% of demand, compared with 15.6% in 1958. Demand was driven by exponential population growth and the rapid spread of suburbs, enabled by universal availability of low cost, minimally taxed gasoline. At the time, no attempt was made to reduce demand by increasing taxes or mandating automobile fuel efficiency. Without increased imports, US production might have peaked even before 1966, regardless of the value of Qmax.
Even if the easily accessible reserves had been as great as 350 billion bbl, peak production (at about 15 million b/d, from Equation 2, lower than actual demand in 1973) would have been delayed by only 12 years, to 1982, according to Hubbert’s model.
Model limitations
There is no geophysical, physical, or chemical law that compels cumulative production to follow Equation 1. The logistic growth curve has nothing to do with any of the physical or geochemical factors that govern oil flows and well productivity. The bell-shaped curve that some have claimed actually governs10 production has nothing like Newton’s laws or the laws of hydrodynamics as its foundation. Oil production is instead determined by a wide variety of physical, political, and economic factors. While one cannot exceed the maximum possible flow rate, flow can be kept well below this maximum for a variety of reasons.
Yet Hubbert’s model did predict the time interval when US oil production peaked. It is important to understand why it did succeed and under what conditions Hubbert’s model might be valid.
Some of the economic and political factors necessary for Hubbert’s model to be applicable are:
- Affordable prices for consumers and good profitability for owners of the resource.
- Stable markets (stable political and market rules).
- Exponentially increasing consumption.
- Perception of limitless resources by producers and consumers; availability of imports.
- Reasonable estimates of the magnitude of easily accessible resources (proven, undiscovered, and reserve extension) given certain extraction costs, profit levels, and technology developments over the forecast period.
These elements of what might be considered an econometric model with political constraints will be examined in more detail in the second part of this article next week.
References
- Anderson, R.O., “Fundamentals of the petroleum industry,” University of Oklahoma Press, 1984. p. 23.
- Weaver, J.L., “Unitization of oil and gas fields in Texas: A study of legislative, administrative, and judicial policies,” Resources for the Future, Johns Hopkins University Press, p. 39.
- Oil production has peaked or reached a plateau in 68 of 99 producing countries, Smith, M.R., quoted in OGJ, May 24, 2004, p. 7.
- Maugeri, L., “Oil: Never cry wolf -why the petroleum age is far from over,” Science, Vol. 304, May 21, 2004, pp. 1114-1115.
- Editorial, “Serious about depletion,” OGJ, Aug. 23, 2004, p. 17.
- Hubbert, M.K., “Nuclear energy and fossil fuels,” American Petroleum Institute Conference, San Antonio, Mar. 7-9, 1956. Later published as Publication No. 95, Shell Development Co., June 1956.
- Hubbert, M.K., “Energy resources, a report to the committee on natural resources of the NAS-NRC,” Publication 1000-D, NAS-NRC, 1962.
- API, “Petroleum facts and figures 1950,” 9th Edition, 1951, p. 117.
- Department of Energy-Energy Information Administration, “Annual energy review (2002),” 2003.
- Campbell, C.J., “The Golden Century of Oil 1950-2050: The Depletion of a Resource,” Kluwer Academic Publisher, Dordrecht, 1991, p. 47.
The author
Alfred J. Cavallo is an energy consultant based in Princeton, NJ, and a physicist with the US Department of Homeland Security Environmental Measurements Laboratory. He holds PhD and MS degrees in physics from the University of Wisconsin (Madison) and a BS from Stevens Institute, Hoboken, NJ. After graduation he spent 6 years in Europe, working first for the Max Planck Institute for Plasma Physics in Munich and then for the French Atomic Energy Commission in Paris on nuclear fusion experiments. He returned to the US in 1981 to work at the Princeton Plasma Physics Laboratory, where he continued in the experimental fusion program. He later moved to the Center for Energy and Environmental Studies at Princeton University, working on indoor air quality and on renewable energy integration issues. He has also done research on aerosols, dose to the lung from radioactive particulates (radon progeny and radon in uranium mines), and regulatory risk. He has become interested in resource constraints on fossil fuels, particularly petroleum and natural gas, in an attempt to understand how renewable energy can compete with such resources and any impact such constraints might have on US security.