New methods for CP design offered
Two new methods for designing pipeline cathodic-protection systems employ newly developed CP design software for marine pipelines.
One method is based upon the recently developed Slope Parameter; the second, upon an inclusive potential attenuation and anode-current-output determination equation. The discussion here shows that the attenuation equation can be applied to both marine pipelines with galvanic bracelet anodes and to buried pipelines with offset anodes and impressed current CP.
The new CP design software is based upon these two attenuation representations.
Corrosion control
An important aspect of ensuring and maintaining pipeline performance is adequate control of corrosion: internal, which is affected by product, and external, which is affected by exposure to soils and waters.
While such control can be achieved by selection of corrosion-resistant-alloy pipe material (intrinsic corrosion control), economic considerations usually dictate that some grade of structural or high strength steel be used. Such cases require extrinsic measures. Internal corrosion is normally managed by product pretreatment with inhibitors; external by a combination of coatings and cathodic protection.
Indicative of the challenges for maintenance is a recently completed study that placed the annual direct cost of pipeline corrosion in the US alone at about $7 billion.1 Such indirect costs as loss of product, environmental and property damages, and loss of life push this figure much higher.
A dual approach to control of external pipeline corrosion is necessary because coatings invariably exhibit defects; and even if this barrier layer can be certified as defect-free at the time of construction, deterioration with time leads to localized exposure of the substrate steel. While CP can, in theory, function as a standalone corrosion-control method, it is only practical when employed in conjunction with a coating.
In effect, CP needs only to provide protection at coating defects. Consequently, the pipe-current demand is low compared with the bare metal case, and therefore anode or anode ground bed spacing can be relatively large.
For example, design of CP systems for marine pipelines normally assumes several percent coating bare area and utilizes galvanic bracelet anodes spaced about 250 m apart. Here, limitations on the size of bracelet anodes that can be structurally supported by the pipe and deployed from a lay barge and CP design life control spacing.
For the onshore buried counterpart, on the other hand, higher coating quality in conjunction with impressed current CP, the type normally employed here, is such that metallic path ground return resistance is controlling; and, consequently, anode ground bed spacings can be as great as 50-100 km.
Fig. 1 schematically shows the potential profile that results in each of these two cases. Thus, for the galvanic bracelet anode situation (Fig. 1a), potential is constant except within the field of the anode with the magnitude of polarization being determined by electrolyte resistivity, anode dimensions, and pipe current demand.
Buried pipelines with impressed current CP and large anode or anode-bed spacings, on the other hand, exhibit a continued polarization decay with increasing distance beyond the field of the anode (Fig. 1b).
As such, generalized pipeline polarization behavior reflects influences from four resistance terms: the anode, coating, pipe polarization, and metallic path return. The critical design feature in the galvanic anode CP case is projection of pipe current demand. For buried pipelines with impressed current CP, anode bed design and spacing are also important.
Pipeline CP design
For marine pipelines with closely spaced galvanic anodes so that metallic path resistance is negligible, the design process has historically involved2 3 Step 1: calculation of net pipe current demand (Ic; Equation 1 in accompanying box) and Step 2: determination of the net anode mass (M in kg) from a modified form of Faraday's law (Equation 2).
Current output of an individual anode (Ia) is calculated by Equation 3 where, for bracelet anodes, Ra is normally calculated with McCoy's formula.4
The number of anodes is then determined by Equation 5, which, in turn, defines their spacing.
A limitation of this protocol is that it cannot be applied to situations in which metallic path resistance is not negligible. Also assumed is that ic and, hence, øc are uniform, both circumferentially and axially.
For marine pipeline CP retrofits, marine pipelines deployed by reeling with subsequent anode sled placement, and buried onshore pipelines with impressed current CP systems, anode spacing is likely to be large and metallic-path resistance significant, as discussed previously. For this circumstance, the classical equations of Morgan5 and Uhlig6 are normally utilized. Thus, Equations 6 and 7 are for pipelines polarized by identical, equally spaced anodes.
A difficulty is that anode resistance does not appear explicitly in Equations 6 and 7 such that if the pipe or a portion thereof lies in the anode potential field, over-protection may result in the near-field and under-protection in the far. This limitation can be partially overcome by independent calculations to determine the drainage point potential (Ea, Equation 7).
Also assumed in application of Equations 6 and 7 and in Equations 1-5 is that coating quality and electrolyte (soil or water) resistivity are uniform and that coating defects are uniformly distributed and sufficiently small that electrolyte-to-pipe potential field is nil. As such, these approaches represent a global approach to pipelines CP design.
Numerical methods are now becoming available7-9 that address the above limitations and allow for inclusion of localized pipe inhomogeneities, electrolyte variations, and effects of stray currents. As an alternative to the above options, this article describes recently developed equations and a design methodology that improve on the global approach.
Also, a software program for design of marine pipeline cathodic protection systems is introduced and reviewed.
Recent equations
Bethune and Hartt10 adapted the Slope Parameter (SP) method11-14 to pipelines with bracelet anodes and projected the governing equation as shown in Equations 8 and 9.
Table 1 lists a relatively broad range of a•γ values, as determined for various combinations of coating quality and current-density demand. Design life, on the other hand, was given by Equation 10.
Iterations can be performed between Equations 7 and 10 in order to optimize the design life. Subsequently, Equation 9 was modified15 to include the resistance of the metallic pipe return path as shown in Equation 11.
Lysogorski and Hartt16 derived a generalized, first-principles-based attenuation equation for pipelines with equally spaced, identical offset anodes that incorporated all relevant resistances: anode, coating, pipe polarization, and metallic path return (Equation 12).
For pipelines with galvanic bracelet (superimposed) anodes, Equation 12 reduces to Equation 13.17
Both equations have been solved with a Coordinate Mapping Based Finite Difference Method (CoMB-FDM) numerical procedure, as explained previously.15 16 Fig. 2 shows potential attenuation plots, as determined by Equation 13, in comparison with results from boundary element modeling (BEM) and Equation 6 for a 0.136 m (5 in.) OD pipeline with identical 60-kg bracelet anodes (øa = –1.05 VAg/AgCl) in a 0.30 Ω·m resistivity electrolyte with L = 122 m and a•γ = 4, 20, 100, and 1,000 (Table 1).
These generally conform to the trend that Fig. 1a illustrates. The close correspondence between results for the first two methods confirms accuracy of Equation 13 since, for such a small L, Rm›0. Further, more quantitative verification appears elsewhere.16 Obviously, the solution of Uhlig6 provides poor correlation except at a·γ = 1,000 Ω·sq m because of its not incorporating anode resistance.
Because Equations 12 and 13 were developed for galvanic anodes CP, their application to pipelines with impressed current systems requires determination of potential of an equivalent galvanic anode that provides the same polarization as the impressed current one (øa(eq)).
This can be accomplished from Equation 14.14 As written, this equation neglects any voltage drops in the rectifier-to-anode(s) cabling. This can be handled, however, by adding a third term to the right side.
Equation 13 was used to determine potential attenuation and anode current output for the specific pipeline and CP system conditions listed in Table 2.
This was done, first, by determining the CP current by solving Equation 14 for the case of a superimposed anode with øa = øa(eq), second, by using this current to determine the drainage point potential, that is, the potential at the initial Δz increment from z = 0, and, third, by solving Equation 13 using the same CoMB-FDM that was developed for Equation 12.16
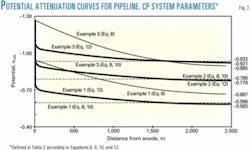
Fig. 3 shows the results for these examples (baseline [corrosion] potentials –0.30 VCSE [Example 1], –0.50 vCSE [Example 2], and –0.65 vCSE [Example 3]), as plots of potential vs. distance from the drainage point. As in Fig. 2, only the z = 0 to L regime is illustrated because, with identical, equally spaced anodes, a mirror image profile results beyond these two limits. Table 1 facilitates gauging the coating quality-current demand combinations that could yield the a•γ value of 17,500 Ω•sq m that was employed.
As an example, this current density demand is achieved by a coating bare area of slightly greater than 0.1% and an ic of 20 ma/sq m. Table 3 lists the anode current output and drainage point potential for each of the three cases. These data indicate that CP current was greater, drainage point potential more positive, and attenuation greater the more positive the native pipe potential. The attenuation behavior was affected by, first, the pipe current demand (constant for the three cases) and, second, anode-pipe potential difference.
In each of the three Equation 12 potential attenuation curves, a "knee" is apparent at z ≈ 500 m. This reflects an influence of the voltage drop associated with both Rm and ρe at lesser distances, indicating that for this region the pipeline remains in the potential field of the anode. At greater distances, however, attenuation is affected solely by Rm.
Fig. 3 also shows pipe potentials projected by Equation 6 (Examples 1 and 3 only for clarity) and Equations 8 and 10. In the former case, a monotonic potential decay is apparent, consistent with exclusion of the potential drop associated with the anode, as well as a non-conservative projection with regard to protection results.
Although slightly nonconservative, the results from Equations 8 and 10 agree well with those from Equation 12 in the far-field. This apparently occurred because of the assumption in the SP method that current density is uniform along the pipe length.
Good agreement can be realized between Equations 6 and 12 if the drain point potential, rather than that of the anode, is used in the former.
The far field potential values indicate that polarization by about 250 mv resulted in each of the three cases. Accordingly, protection has been affected based upon common magnitude-of-polarization criteria (100 mv polarization, for example). Thus, either anode spacing could be increased or rectifier voltage decreased and protection still be realized.
The latter is preferred, however, for the two more negative corrosion potential cases (Examples 2 and 3) because of the relatively negative drainage point potential that resulted here and the possibility of coating damage or hydrogen embrittlement (or both).
A more positive drainage point potential could also be realized by increasing the anode offset distance. By successive design modifications and Equation 12 calculation iterations, the CP design can be optimized.
Software
With the SP method (Equations 8, 10, and 11) and the Inclusive Equation (Equation 12), a CP design software package has been developed using Microsoft Visual Basic 6.0 for Windows-based applications that is applicable to both new and retrofit marine pipelines as well as to pipelines that are deployed by reeling.
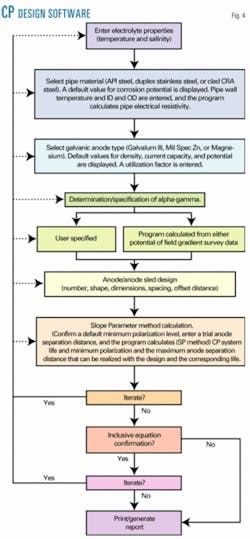
Fig. 4 shows a flow diagram for this in which various environment, pipe and anode material, and CP design parameters are either entered or calculated from input values. This includes a value for pipe current-density demand, as either a design choice or in the case of retrofits as calculated from pipe potential or field gradient survey data that were acquired before any significant depolarization.
In the case of a new pipeline, such survey data may be from a similar vintage pipe in the same general location. The user specifies either a single or multiple anodes, in which the latter conform to either a linear or rectangular, equally spaced array.
An algorithm based on Sunde's equation19 calculates the net array resistance with anode dimensions, separation distance, and offset distance from the pipe serving as inputs. Boundary Element Modeling has indicated that the algorithm yields a solution for array resistance that is conservative by no greater than 12%.20
Based upon the Slope Parameter Method (Equations 8 and 11), the various entered and calculated parameters, and an entered value for the minimum acceptable polarization (mid-anode spacing value), the program indicates the maximum allowable anode spacing and the corresponding design life.
Using this information as a guide, the user enters a trial anode spacing, and the program calculates the resulting pipe potential and design life. Iterations may be performed to optimize the design.
Fig. 5 shows a computer screen's display of this step based upon a retrofit marine steel pipeline CP design that utilizes Al-Zn-In anodes and the parameters in Table 4. This view consists of a toolbar near the top with various icons that open specific design data input and calculation windows, in addition to standard ones (file, save, and print). It is from the input data and parameters that the different program calculations are generated.
The viewing area in Fig. 5 also shows retracted windows titled "Medium Property," "Pipeline Property," "Anode Property," "Alpha and Gamma," and "Anode Array," in addition to the open window ("Design by Slope Parameter").
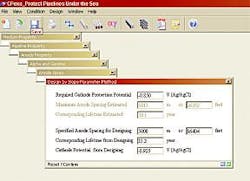
Fig. 6 shows a closer view of this open window, in which the uppermost box indicates the user-selected most positive design polarized pipe potential (mid-anode spacing value). Upon this being entered, values for the maximum allowable pipe potential and corresponding design life that will achieve the selected polarization are displayed in the subsequent two boxes.
The user then enters a design anode spacing (5,000 m in this case, fourth box), and, upon execution, the corresponding design life and maximum or mid-anode spacing potential are displayed (bottom two boxes, respectively).
The user then has the option of generating an Inclusive Equation (Equation 12) based plot of the attenuation profile and comparing this with the Slope Parameter calculation result. Generating this plot is recommended because doing so provides a more complete understanding and greater accuracy than the SP calculation result alone.
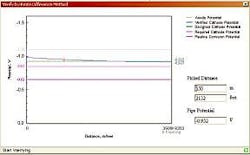
Fig. 7 shows graphically the results from executing this option. The figure includes a plot of potential vs. distance to the mid-anode spacing value (2,500 m). Also shown are horizontal lines corresponding to an assumed or measured value for the pipe free corrosion potential (–0.65 v), the result of the Slope Parameter calculation from the previous window (green horizontal line at potential at –0.925 v, bottom-most window in Figs. 5 and 6) and the anode potential (-1.10 v).
The projected pipe potential profile appears as the blue curve and indicates a relatively gradual potential attenuation from near the anode to a mid-anode spacing value of –0.917 v.
A more abrupt potential gradient near the anode is not apparent because of the compressed scale and large anode spacing. The mid-anode spacing potential indicated by this calculation is 8 mv more positive than from the Slope Parameter one, indicating a degree of non-conservatism for the latter. This presumably resulted because the SP method assumes current density is constant along the pipe length, which it is not.
Fig. 7 also illustrates an option for identifying the pipe potential at a given distance from the anode. In the example illustrated here, the curser was placed at 550 m and clicked. This resulted in display of a red cross-hair on the potential-distance curve at 550 m and this distance and the corresponding pipe potential (–0.952 v) being displayed in the respective boxes at the lower right.
The program provides a relatively simple, rapid, straightforward method for performing marine pipeline CP retrofit designs. New pipe CP designs are accommodated as well. In view of the number of marine pipelines worldwide that either have exceeded or are approaching their design lives and the importance of maximizing anode spacing in CP retrofits of such pipelines, the software offers both a technical and economic advantage to otherwise available options.
Acknowledgments
The authors are indebted to member organizations of a joint industry project, including ChevronTexaco, ExxonMobil Corp., Equilon Pipeline Co. (now Shell Pipeline Company LP), and the US Minerals Management Service for financial sponsorship. Also appreciated is the technical guidance and assistance from members of the technical advisory committee that includes Fred Corsiglia, Russell Lewis, Mark Mateer, Neill Strickland, and Robert Smith.
References
1. Corrosion Costs and Preventive Strategies in the United States," Report No. FHWA-RD-01-156, Federal Highway Administration, Washington, March 2002, pp. 24-25.
2. "Cathodic Protection Design," DnV Recommended Practice RP401, Det Norske Veritas Industri Norge AS, 1993.
3. "Pipeline Cathodic Protection – Part 2: Cathodic Protection of Offshore Pipelines," Working Document ISO/TC 67/SC 2 NP 14489, International Standards Organization, May 1, 1999.
4. McCoy, J. E., Institute of Marine Engineers Transactions, Vol. 82 (1970), p. 210.
5. Morgan, J., Cathodic Protection. New York: Macmillan, 1960, pp. 140-143.
6. Uhlig, H. H., and Revie, R. W., Corrosion and Corrosion Control, Third Ed., New York: J Wiley and Sons, 1985, pp. 421-423.
7. Riemer, D. P., and Orazem, M. E., "Models for Cathodic Protection of Multiple Pipelines with Coating Holidays," proceedings Research Topical Symposium on Cathodic Protection: Modeling and Experiment, NACE International, Houston, 1999, p. 66.
8. Bortels, L., "A User-Friendly Simulation Software for the Cathodic Protection of Large Networks of Buried Pipelines Influenced by Traction Stray Currents," CORROSION/02, Apr. 7-11, 2002, Denver.
9. Bortels, L., "The Use of Dedicated Simulation Software for the Design and Understanding of the Cathodic Protection of Underground Pipeline Networks under Various Interference Conditions," CORROSION/03, Mar. 17-21, 2003, San Diego.
10. Bethune, K., and Hartt, W. H., Corrosion, Vol. 57. 2001, p. 78.
11. Wang, W., Hartt, W. H., and Chen, S., Corrosion, Vol. 52 (1996), p. 419.
12. Hartt, W. H., Chen, S., and Townley, D. W., Corrosion, Vol. 54 (1998), p. 317.
13. "Design of Galvanic Anode Cathodic Protection Systems for Offshore Structures," state-of-the-art report prepared by NACE International Task Group T-7L-16 on Offshore CP Design, NACE International, Houston, 1998.
14. Hartt, W.H., "The Slope Parameter Approach to Marine Cathodic Protection Design and Its Application to Impressed Current Systems," in Designing Cathodic Protection Systems for Marine Structures and Vehicles, Ed. H. Hack, Special Technical Publication 1370, Am. Soc. for Testing and Materials, West Conshohocken, Pa., 1999.
15. Hartt, W. H., and Lysogorski, D., "The Slope Parameter Approach in Design and Analysis of Cathodic Protection Systems," CORROSION/03, Mar. 16-21, 2003, San Diego.
16. Lysogorski, D., and Hartt, W.H., "A Modified Potential Attenuation Equation for Cathodically Polarized Marine Pipelines and Risers," CORROSION/03, Mar. 16-21, 2003, San Diego. To be published in Corrosion.
17. Lysogorski, D., Hartt, W. H., and Ananthakrishnan, P., Corrosion, Vol. 59 (2003), p. 684.
18. Pierson, P., Bethune, K., Hartt, W.H., and Ananthakrishnan, P., Corrosion, Vol. 56 (2000), p. 350.
19. Sunde, E. D., Earth Conduction Effects in Transmission Systems, New York: Dover Publications Inc., 1968, p. 79.
20. X. Zhang, W. Chu, and W.H. Hartt, "An Integrated Approach to Determination of Anode Array Resistance for Cathodic Protection of Marine Structures and Pipelines," 05075 to be presented at CORROSION/05, Apr. 4-8, 2005, Houston.
Based on a presentation to the 6th International Conference on Pipeline Rehabilitation & Maintenance, Oct. 7-9, 2003, Berlin.
The authors
William H. Hartt is professor of ocean engineering and director of the Center for Marine Materials at Florida Atlantic University, Sea Tech Campus, Dania Beach, Fla. He has served on the board of directors of NACE International and has chaired the Unit Committee T7L on cathodic protection in natural waters. For the past 15 years, he has served as principal investigator for a series of joint industry projects addressing design criteria for deepwater petroleum production structures and design of retrofit cathodic-protection systems for fixed offshore platforms and for marine pipelines. Hartt holds a BS (1961) from Virginia Tech and a PhD (1966) from the University of Florida, both in metallurgical engineering.
Wei Chu is a postdoctoral research associate at Florida Atlantic University, Sea Tech Campus, Dania Beach, Fla., and has served as a postdoctoral researcher (2000-02) at the University of South Carolina. He holds a PhD (1999) in physical chemistry from Xiamen University, China.