New correlations calculate volatile oil, gas condensate PVT properties
New correlations provide modified black-oil (MBO) pressure-volume-temperature (PVT) properties when fluid samples are unavailable.
One can use the correlations in generalized material balance calculations and MBO simulations. The new correlations match the fluid properties of a selected database and the authors also validated them with generalized material balance calculations.
To develop the new corrections, the authors modified existing solution gas-oil ratio, oil formation volume factor, and gas formation-volume factor correlations to increase their accuracy when used with gas condensates and volatile oils.
The new correlations have an accuracy within 10.4% for gas condensate and 15% for volatile oil samples used in this study.
MBO approach
Several authors have shown that an MBO approach could replace compositional simulation in many applications for modeling gas condensate and volatile oil reservoirs.
This work developed a new set of MBO PVT correlations. The four PVT functions are:
- Rv, oil-gas ratio.
- Rs, solution gas-oil ratio.
- Bo, oil formation volume factor.
- Bg, gas formation volume factor.
To our knowledge, a correlation for calculating oil-gas ratio did not exist in the petroleum literature. Without this correlation, the analysis required for generating the oil-gas ratio required a combination of laboratory experiments and elaborate calculation procedures using equation of state models.
The new Rv correlation depends on only readily available parameters in the field and can have wide applications when representative fluid samples are unavailable.
Previous work
In 1973, Spivak and Dixon introduced the MBO simulation approach.1 The MBO simulation considers three components; dry gas, oil, and water. The main difference between the conventional black-oil simulation and the MBO simulation, also called extended black-oil, lies in the treatment of the liquid in the gas phase.
The MBO approach assumes that the stock-tank liquid component can exist in both liquid and gas phases under reservoir conditions. It also assumes that one can define the liquid content of the gas phase as a sole function of pressure called vaporized oil-gas ratio, Rv, also referred to as rs2. This function is similar to the solution gas-oil ratio, Rs, normally used to describe the amount of gas-in-solution in the liquid phase.
Whitson and Torp presented a procedure to calculate MBO properties from PVT experimental data of gas condensate.2 Coats also presented a different procedure for gas condensate fluids.3 Coats’s procedure was extended by McVay for volatile oil fluids.4 Walsh and Towler (OGJ, July 31, 1994, p. 83) also presented a procedure to calculate MBO PVT properties from constant volume depletion (CVD) experiment data.5
Fattah et al. (OGJ, Mar. 27, 2006, p. 35) showed that both Whitson and Torp’s and Coats’s procedures provide an excellent match with compositional simulation results when the analysis matches PVT experimental with an EOS model and then uses it to find the MBO PVT properties.6
El-Banbi et al. presented a field case where MBO PVT properties and the MBO approach helped speed a field development plan.7 They presented evidence that the MBO approach adequately simulates gas condensate fluids above and below the dewpoint and with water influx.
Other authors also have presented different comparisons between the MBO and compositional approaches.2 3 6
In recent work, Fevang et al. presented guidelines to help engineers choose between MBO and compositional approaches.8
Fluid samples
The petroleum literature has reported many cases where the MBO approach replaced more expensive compositional simulation. Generating MBO PVT properties requires a representative fluid sample that undergoes enough laboratory experiments. Then, one usually constructs EOS models to match the laboratory experimental results, although there are other less accurate techniques.6
One can output the MBO properties at appropriate separator conditions using one of the procedures suggested in literature. This process requires the availability of a representative fluid sample in addition to the skills of EOS modeling.
The set of correlations presented in this article can generate MBO PVT properties without the need for fluid samples or an elaborate procedure for EOS calculations. The application of these correlations is of particular importance especially when a representative sample is unavailable.
Our study used 13 reservoir fluid samples (8 gas condensates and 5 volatile oils). The samples were from reservoirs at different locations and depth and covered a wide range of oil and gas fluid characteristics.
Table 1 shows the major properties of the 13 fluid samples. Reference 9 presented the PVT experiments for all these samples. Some samples represent near critical fluids (VO 2, VO 5, GC 1, and GC 2) as explained by McCain and Bridges.10
Approach
For every sample in Table 1, we constructed an EOS model that matched as best as possible the experimental results of all available PVT laboratory experiments that included constant composition expansion (CCE), constant volume depletion (CVD), differential liberation (DL), and separator tests.
For consistency, we developed all EOS models using the Peng and Robinson EOS with volume shift correction (three-parameter EOS).11 We followed the procedure suggested by Coats and Smart to match the laboratory results.12
We then used the developed EOS model for each sample to output MBO PVT properties at different separator conditions using Whitson and Torp’s procedure.3
The MBO PVT properties include the four functions required for MBO simulation: Rv, Rs, Bo, and Bg. For each of the four properties, we generated six curves, representing six different separator conditions for each sample.
Our database of PVT properties consisted of 1,850 points from eight different gas condensate samples and 1,180 points from five volatile oil samples.
We used PVTi program of Eclipse to generate the curves for the MBO PVT properties.13
For the three parameters commonly used for black-oil material balance and simulation (Rs, Bo, and Bg), we tested some known correlations to determine the one that fits our database and to see if we needed to modify the correlation constants.
For Rv, we had to develop a completely new correlation because we could not find one in the petroleum literature. Our approach was to start from a similar form to Rs correlations, then modify the correlation parameters using regression methods until we obtained the best fit to Rv data.
MBO PVT correlations
Our analysis used Equation 1 in the accompanying equation box to determine the average error for each of the four PVT parameters.
For Rs the analysis used several correlations for testing the database for both volatile oil and gas condensate samples. We found that the forms suggested by Standing and Vasques and Beggs gave the best results after we modified the correlation constants.14 15 The average absolute error for both gas condensates and volatile oil samples was as high as 50% if we used the original correlation parameters. This probably results from the original Standing and Vasques and Beggs correlations being developed for black oils.16
Equations 2 and 3 show the modified Standing correlation, and Equations 4 and 5 show the modified Vasques and Beggs correlation. Table 2 lists five parameters for the modified Standing correlation, obtained from regression analysis for both gas condensate and volatile oil samples. Table 3 lists the new parameters for the modified Vasques and Beggs correlations.
The average error calculated with Equation 1 was 20.5% for gas condensates and 23.2% for volatile oils. The modified Vasques and Beggs has higher errors of 27.7% for gas condensates and 29.2% for volatile oils.
For volatile oil above the bubblepoint, Rs, the analysis uses the same value as the bubblepoint value.
For calculating Rv, we needed a completely new form for the correlation. A useful correlation with a wide applicability has to have parameters with readily available values without the need for fluid samples or elaborate calculation procedures using EOS models.
Equation 5 is the derived correlation. The absolute average error with this form is 10.4% with a standard deviation of 0.0308 for gas condensates and 15.0% with a 0.1271 standard deviation for volatile oils.
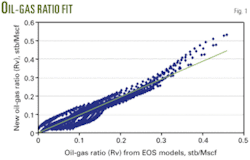
Table 4 shows the correlation constants A1 to A5. Fig. 1 is a cross plot for all gas condensate points and shows the 45° line, as an indication of the goodness of fit for the calculated results vs. experimental results. Notice that initial condensate yield, which can be obtained from production data, depends on separator conditions in the field.
One can determine saturation pressure from a pressure vs. cumulative production plot. The saturation pressure is observed by change in slope in this plot due to the difference in depletion above and below the saturation pressure, or from constant composition expansion on a representative sample.
The Rv value is constant above the dewpoint for gas condensate samples.
For the oil formation volume factor, Bo, the analysis tested several correlations against the database of Bo points for both the gas condensate and volatile oil samples below the saturation pressure. It was found that one can use adequately both the Standing correlation and the Vasques and Beggs correlation (absolute average errors about 4%) without modifications. One can improve the error percentage of Bo with the constants listed in Table 5. Equation 6 gives the modified Standing correlation.
Equation 6 has an average absolute error of 2.7% for gas condensate samples and error of 1.6% for volatile oils. Further testing of the modified Bo correlation showed that it was not greatly affected by the accuracy of the Rs values used.
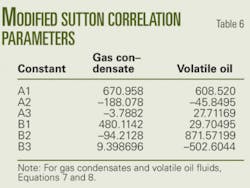
One can calculate Bg from the z-factor. We tested the use of the Sutton correlation to calculate pseudocritical properties and then used the Standing z-factor correlation in a calculation procedure suggested by Dranchuk and Abou-Kassem.17 18 We found this procedure for calculating Bg adequate for both the gas condensate and volatile oil samples (absolute average error less than 8%). The correlation, however, improves with the use of different Sutton parameters, as in Equations 7 and 8.
Table 6 lists the values for the modified Sutton equation. The analysis obtained these parameters by minimizing the error given by Equation 1.
We used the pseudocritical properties from Equations 7 and 8 to calculate the z-factor and then Equation 9 to obtain Bg.
The average absolute error in Bg, with this procedure, is 3.8% for gas condensate and 1.65% for volatile oil samples. Notice that the gas specific gravity used in the modified Sutton correlation is corrected for separator conditions with Equation 4.
Correlation validation
In addition to cross plots, such as Fig. 1, to see how the new correlation values compared to the values obtained from the EOS model, we validated the new corrections with reservoir simulation and material balance calculations.
We used the generalized material balance equation from Walsh to validate the new Rv correlations by performing the material balance calculations using the PVT properties from the new correlations to calculate original hydrocarbon in place.19 20 We compared these values to the original hydrocarbon in place values obtained from compositional reservoir simulation for a tank model.
For simplicity, the analysis normalized the original fluid in place to 1.0 billion stock-tank bbl for oil cases and 1 bscf for gas cases.
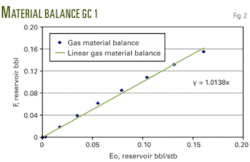
Fig. 2 shows a plot of F vs. the expansion term, Eg, for a gas condensate sample (GC 1), based on the Walsh procedure. The slope of the line passing through the calculated points gives the original fluid in place volume. The plot shows that the slope of the line is 1.038, with the error in gas in place calculation of about 1.4%.
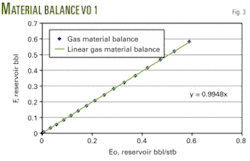
Fig. 3 is a similar plot for the volatile oil sample (VO 1). The plot shows a slope of 0.9948, which is equivalent to the error in the oil in place calculation of about 0.5%.
Table 7 shows the error in the calculated fluid in place for most of the fluid samples in our database. The error values show high accuracy and prove the validity of the new correlations.
Acknowledgments
The authors thank Schlumberger Egypt for donating the Eclipse suite of software, used in this investigation, to the petroleum engineering department of Cairo University. In addition, A.H. El-Banbi also thanks Bill McCain for many valuable discussions that led to this research.
References
- Spivak, A., and Dixon, T.N., “Simulation of Gas Condensate Reservoirs,” Paper No. SPE 4271, 3rd Numerical Simulation of Reservoir Performance Symposium, Houston, Jan. 10-12, 1973.
- Whitson, C.H., and Torp, S.B., “Evaluating Constant-Volume Depletion Data,” JPT, March 1983, pp. 610-20.
- Coats, K.H., “Simulation of Gas Condensate Reservoir Performance,” JPT, October 1985, pp. 1870-86.
- McVay, D.A., Generation of PVT Properties For Modified Black-Oil Simulation of Volatile Oil and Gas Condensate Reservoirs, PhD Thesis, Texas A&M University, 1994.
- Walsh, M.P., and Towler, B.F., “Method Computes PVT Properties for Gas Condensate,” OGJ, July 31, 1994, pp. 83-86.
- Fattah, A., et al., “Study Compares PVT Calculation Methods for Non Black Oil Fluids,” OGJ, Mar. 27, 2006, p. 35.
- El-Banbi, et al., “Producing Rich-Gas-Condensate Reservoirs—Case History and Comparison Between Compositional and Modified Black-Oil Approaches,” Paper No. SPE 58988, SPE Fourth International Petroleum Conference and Exhibition, Villahermosa, Mexico. Feb. 1-3, 2000.
- Fevang, O., et al., “Guidelines for Choosing Compositional and Black-Oil Models for Volatile Oil and Gas-Condensate Reservoirs,” Paper No. SPE 63087, SPE ATCE, Dallas, Oct. 1-4, 2000.
- El-Fattah, K.A., Volatile Oil and Gas Condensate Fluid Behavior for Material Balance Calculations and Reservoir Simulation, PhD Thesis, Cairo University, 2005.
- McCain, W.D., Jr., and Bridges, B.: “Volatile Oils and Retrograde Gases-What’s the Difference?” Petroleum Engineer International, January 1994, pp. 35-36.
- Peng, D.Y., and Robinson, D.B., “A New Two-Constant Equation of State” Ind. and Eng. Chem. Fund, 1976, p. 59.
- Coats, K.H., and Smart, G.T., “Application of a Regression-Based EOS PVT Program to Laboratory Data,” SPERE, May 1986, pp. 277-99.
- ECLIPSE suite of programs, Schlumberger, 2005.
- Standing, M.B., “A Pressure-Volume-Temperature Correlation for Mixture of California Oils and Gases,” Drilling and Production Practice, API, 1957, pp. 275-87.
- Vasques, M., and Beggs, H.D., “Correlation for Fluid Physical Property Prediction,” JPT, June 1980, pp. 968-70.
- Ahmed, T., Hydrocarbon Phase Behavior, Houston, Gulf Publishing Co., 1989.
- Sutton, R.P., “Compressibility Factors for High-Molecular-Weight Reservoir Gases,” Paper No. SPE 14265, SPE ATCE, Las Vegas, Sept. 22-25, 1985.
- Dranchuk, P.M., and Abou-Kassem, J.H., “Calculation of Z Factors for Natural Gases Using Equations of State,” JCPT, July-September 1975, pp. 34-36.
- Walsh, M.P., “A Generalized Approach to Reservoir Material Balance Calculations,” JCPT, 1994.
- Walsh, M.P., et al., “The New Generalized Material Balance As an equation of a Straight-Line: Part 1—Application to undersaturated and Volumetric Reservoirs,” Paper No. SPE 27684, SPE Permian Basin Oil and Gas Recovery Conference, Midland, Tex., Mar. 16-18, 1994.
The authors
K.A. Fattah ([email protected]) is assistant professor in the petroleum and natural gas engineering department, King Saud University, Riyadh. He previously was a professor at Cairo University. He also is a consultant engineer in reservoir simulation, and directional and horizontal drilling. Fattah holds a BSc, an MSc, and a PhD in petroleum engineering from Cairo University.
Ahmed El-Banbi ([email protected]) is a data and consulting services manager for Schlumberger Inc. in Cairo. He previously was a professor at Cairo University. El-Banbi holds a BS and an MS in petroleum engineering from Cairo University and an MS and PhD in petroleum engineering from Texas A&M University.
M.H. Sayyouh ([email protected]) is the previous chairman of the mining, petroleum, and metallurgical department, faculty of engineering, Cairo University. He also is a consultant engineer in reservoir simulation and enhanced oil recovery. Sayyouh holds a BSc and an MSc in petroleum engineering from Cairo University and a PhD in petroleum and natural gas engineering from Pennsylvania State University. He is a member of SPE.