Options approach aids development decision for Colombian field
An options evaluation approach aided Empresa Colombiana de Petróleos (Ecopetrol), Colombia's state-owned oil company, in making a decision on whether to participate in developing the newly discovered Guando field.
In June 2002, the Guando staged development plan, submitted by license operator Petróleo Brasileiro SA (Petrobras), 30% working interest, and partner Nexen Inc., 20%, awaited Ecopetrol's approval.
If Ecopetrol, holding the remaining 50% working interest, elected not to participate in the development plan, its partners had the option to develop the field under the sole-risk provisions in the Boqueron Association Contract.
Guando development plan
Guando field (Fig. 1), discovered in 2000, represented a new geological play in the Guadalupe formation (Cretaceous) of the Cordillera basin. It was the first reservoir discovered in this play and thus opened up new opportunities in the area for exploration and development.
Because the field is at a shallow 1,060-m depth, however, it has low reservoir pressure. This implies that the field will require water injection for raising and maintaining reservoir pressure to optimize oil producing rates and ultimate recovery.
Conventional discounted cash flow (DCF) analysis, with conservative oil price assumptions, indicated that the development had marginal or negative economics. Ecopetrol's initial decision regarding participating in the development hinged, in part, on the success of a pilot waterflood that was incorporated in the staged development plan.
Ecopetrol's initial decision (Decision 1) involved several possible outcomes and required evaluating future options and decisions associated with this staged plan.
In the plan, the pilot waterflood would inject 15,000 b/d of fresh water from the Sumapaz river, about 10 km from the field, through three injection wells that initially would affect six producing wells within an inverted seven-spot pattern.
Initially the pilot would provide only formation injectivity information. Crucial information about the sweep efficiency and oil recovery would become available only after 2 years of production.
The plan also included 10 additional peripheral injection wells for extending the pilot across the field. These wells would inject an additional 15,000 bw/d into the edge of the field, 6 months after the start of the pilot but before the availability of the information on sweep efficiency.
The peripheral wells would have the objective of increasing reservoir pressure by at least 100 psi. The plan also included completing 18 additional oil producing wells.
Two years after starting the waterflood pilot, Ecopetrol would have to make a second decision (Decision 2) on whether to continue the staged plan. The plan at this point called for increasing injection to 50,000 bw/d and drilling 17 additional infill injection wells.
Ecopetrol could make the decision to proceed or reject this infill scheme based on the results of the pilot and peripheral injection programs that would provide information of such factors as sweep efficiency, average water injection per well, operational issues and costs, and prevailing oil prices.
The staged plan would have a total of 44 production wells in the initial phase and 66 wells by yearend 2004.
Uncertainties
In addition to establishing the sequence and definition of the stages, it is crucial to identify and evaluate the uncertainties associated with each stage. Waterflooding is a proven and successful technique that has enhanced oil recovery in many fields, although it is not applicable to all reservoirs.
A common problem is the incompatibility of the injected water and the reservoir formation. This can lead to mineral deposition and alterations that can plug pores and reduce permeability, thereby reducing well productivity and injectivity. A loss in injectivity can lead to mechanical failures related to high injection pressures. Filtering the source water and treating it with additives, such as potassium chloride, are options that can reduce the risk of plugging.
Another problem is that injected water could enter preferentially into the underlying aquifer and bypass the oil zone. This more likely would happen from the peripheral injection wells.
The initial 2-year pilot and peripheral waterflood would provide information on how these uncertainties affect sweep efficiency. Until this information became available, the success of the waterflood would remain uncertain.
Future product prices always create a high uncertainty for upstream oil and gas projects. Because of oil price volatility, many companies, including Ecopetrol, prefer to use conservative future oil prices in project evaluations.
For the Guando crude, Ecopetrol adopted a flat $16/bbl West Texas intermediate oil price discounted by $2.
The analysis also incorporated an annual standard deviation of 43.5% in the oil price, based on historical oil price volatility.
Options approach
Conventional DCF analysis often fails to account satisfactorily for uncertainty and management flexibility in selecting alternative options. This is particularly true when companies use single-case deterministic analysis for evaluating projects.
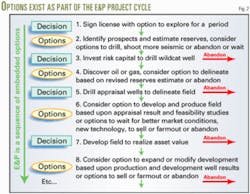
Fig. 2 highlights how an analysis can consider most exploration and production projects as a series of embedded options. Simple DCF valuation models often are flawed if management ignores to evaluate these options.
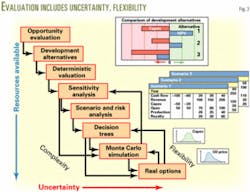
The methodology shown in Fig. 3 suggests that more sophisticated economic evaluation techniques become desirable as project uncertainty, complexity, and resource availability increase. Such techniques can improve significantly the quality of the valuations, the insight to key uncertainties, and the ability to incorporate flexible decisions in a staged project. Each technique identified in Fig. 3 builds upon, rather than replaces, the prior ones and their results.
This article presents the results of decision tree and simple (European call) real-options analyses of the Guando field development from Ecopetrol's perspective. It illustrates how such techniques can provide significant insights to project uncertainties and the value of flexibility.
A real-options approach goes beyond the basic numerical analysis of financial options equations pioneered by Black and Scholes1 and Merton.2 But it is beyond this article's scope to discuss in-depth the many uses of real options for enhancing analysis and valuing industrial projects, including the more complex American call options and simulation analysis.3-5
Building decision trees
Decision trees offer an excellent means of identifying project options and framing the logical sequence of decisions required for specific but uncertain outcomes in an options context. They also offer a means for assigning probabilities, albeit subjectively, to each specific outcome. This is both a strength and weakness of the technique.
Decision-tree analysis involves constructing a framework to represent the logical interrelationships between decisions and outcomes.
A traditional deterministic DCF calculation of net present value (NPV) or a simulation analysis that incorporates additional uncertainties in a stochastic calculation can find the value of each tree branch.
In both analyses, the discount rate employed is usually the company's weighted average cost of capital, which remains constant during all project stages. This ignores such factors as exploration projects having a higher cost of capital than proved-reserves development projects.
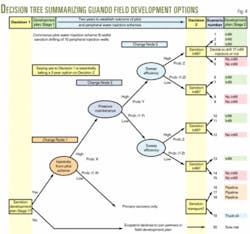
Decision-tree nomenclature identifies decision nodes (squares in Fig. 4) that are associated with management decision options and chance nodes (circles or ovals) that are associated with probabilistic outcomes.
The analysis establishes the value of the alternative options associated with specific decision points by calculating the expected values (EV) for each decision tree branch, leading from right to left into that decision point (EV = probability of occurrence times NPV). The decision rule usually applied to decision trees is that rational managers will always select the branch (alternative) with the highest EV.
Fig. 4 illustrates a decision-tree framework incorporating 20 different possible ultimate outcomes identified by the project engineers associated with the two decision points of the staged Guando development program incorporating a flexible waterflood scheme.
Probabilities for each chance node branch of the decision tree were established with a panel of technical experts incorporating:
- Ecopetrol professionals that have been involved the defining and evaluating the Guando project since field discovery.
- Knowledge and experience captured and retained by Ecopetrol from similar projects and reservoir formations in Colombia and North America.
This rigorous and systematic approach encountered objectivity issues concerning the high levels of uncertainty associated with the future outcomes. It was difficult for experts to agree on the probabilities that should be assigned to each branch of the tree, and the probability values assigned must be recognized as approximations at best.
This is not unusual when defining complex outcomes in a decision-tree framework. It was therefore prudent to conduct sensitivity analysis associated with the probability values assigned to probabilities X, Y, Z, and S (Fig. 4 and Table 1).
Dynamic decision trees, a combination of decision trees and Monte Carlo simulation, offer a comprehensive way to compute such probabilities from the uncertainties modeled, avoiding this problem.
Uncertainty associated with the time at which sufficient data become available to establish which of the 20 outcomes analyzed would materialize also concerned the technical experts of both Ecopetrol and its partners. Two years was the timeframe eventually agreed upon as the most likely period required for making the decision associated with the infill waterflood program.
Flexibility, however, was introduced into this timeframe with the provision that Decision 2 might be delayed because of unforeseen eventualities, market conditions, or ambiguous results from the pilot and peripheral water flood programs. Such flexibility equates to an option to wait.
Table 1 lists the actual probability values for X, Y, Z, NPVs, and probabilities for each of the 20 outcomes defined for the decision tree in Fig. 4. Rows 1-20 correspond with scenario Outcomes 1-20 in the decision tree.
A common practice is to illustrate these values at the appropriate nodes on the decision tree. This is done for part of the tree in Fig. 5. The tabular form, however, is included in the interest of space and to facilitate convenient comparisons and sensitivity analysis.
The NPVs in Table 1 used Ecopetrol's 11%/year corporate risk-adjusted cost of capital as a discount rate, a conservative $16/bbl flat oil price for the entire project life, and a fiscal model applicable to Ecopetrol's contractual position in the Guando field.
Establishing optimal decision set
Once production from Stage 1 of the development plan has continued for about 2 years, Decision 2 associated with sanctioning or rejecting the infill waterflood program must be made. Table 1 illustrates how it is possible to establish the optimal set of decisions for the field development by "rolling back" the tree from the right-hand side and comparing the weighted average NPVs (EVs) at each decision node. The highest EV branch is selected according to the conventional decision rule and other branches are rejected.
The valuations for each branch are clear-cut in most cases (Column D in Table 1). The decision choice, however, is ambiguous for the primary recovery Outcomes 16-18 (install a pipeline-weighted average NPV), and Outcome 19 (truck oil-NPV). Both outcomes have negative EVs with the pipeline NPV being slightly less negative. The evaluation would require a sensitivity analysis to confirm that a pipeline is the better option.
Table 1 shows the derivation and comparison of the two branch values emanating from Decision Node 1 (far left in Fig. 4). If Ecopetrol rejects the development plan and permits the partners to proceed on a sole-risk basis, the contract provisions allow the partners to recover 200% of their capital investment before Ecopetrol becomes entitled to receive, at its option, 50% of positive operating cash flows.
The sole-risk option enables Ecopetrol to avoid participating in risk capital, but significantly limits its future cash flow from the project. Table 1 clearly indicates that Outcome 1 is the most favorable, generating positive cash flow on a sole-risk basis. The other outcomes result in negative cash flows when 200% of the investment capital is deducted.
The sole-risk value to Ecopetrol for this low oil price case is $1.8 million. If Ecopetrol elects to participate in the development plan (says "yes" to Decision 1) then Table 1 shows the EV for that decision branch, incorporating weighted average NPVs for all the other 19 outcomes (except sole risk), is $37.7 million.
The decision rule, based on the assumptions in this model, indicates Ecopetrol should say "yes" to Decision 1 because the $37.7 million is significantly greater than the $1.8 million.
It is important to test the model with sensitivity cases. Table 2 shows the sensitivity analysis results associated with probabilities for the $16/bbl oil price. It shows that the waterflood development plan exceeds the value of the sole-risk option from Ecopetrol's perspective for values of Probability X as low as 0.25. This probability means that there is only a 25% chance that the injectivity tests will succeed.
In projects that require less capital investment, a sole-risk option often is the favored alternative and represents a valuable option available to the state-owned company.
Outcomes 16-19 in Table 1 are for primary-recovery scenarios. These clearly are uneconomic at a $16/bbl oil price. Sensitivity analyses indicate that these scenarios become economic at an $18/bbl minimum constant oil price. Outcomes 1-12 and 14-16 involve additional recovery of probable and possible secondary reserves or better reservoir performance. Stage 1 in the plan can be seen as an attempt to prove up the probable and possible reserves.
Ecopetrol, historically, has included only the proved developed and undeveloped reserves in its economic evaluation for deciding on sanctioning or rejecting its participation in a field development for licenses controlled by association contracts. Incorporating probable and possible reserves into its analysis was a new departure for Ecopetrol. It was therefore essential for Ecopetrol to analyze the waterflood components separately because these outcomes provide the most uncertainty.
The last column of Table 1 calculates the outcome values that influence Decision 2 after the pilot waterflood confirms the benefits of a secondary-recovery development for the entire field. Fig 5 also illustrates this analysis.
Both Table 1 and Fig. 5 show the derivation of the $40.3 million EV for Decision 2.
Progressing analysis
Ecopetrol, traditionally, has used DCF analyses as its main valuation and decision-making tool. It employs more complex tools such as decision trees and Monte Carlo simulation for situations requiring additional analysis for improving the decision-making process.
Real options allow the capture of the value of management flexibility in a way that NPV and static-deterministic decision tree analysis cannot achieve easily, even if each branch outcome is based on a simulation model.
DCF computations normally include the most probable scenario and are discounted at a constant discount rate, in spite of the fact that uncertainty changes and cost and sources of capital may vary as a project evolves.
Moreover, static decision trees assume that decisions during the entire project life are fixed and therefore ignore opportunities to modify decisions as project uncertainties resolve.
Incorporating a real-options component in dynamic decision-tree calculations somewhat overcomes this problem.6 The combination of real options with a decision tree display helps the decision-maker map potential outcomes and decisions and their logical relationships in time.
The close relationships between decision trees and real-options valuation means that once an analysis establishes a decision-tree framework, it becomes relatively easy to extend the analysis to include real options.
Applying real options
A real-options approach to valuing this secondary-recovery project is interesting because of the high uncertainty associated with the future outcomes and because the project will gain new and more precise information as it proceeds. This approach may therefore provide management with a way to respond more effectively to new information concerned with well injectivity and reservoir sweep efficiency.
The negative economics for developing the field with primary-recovery methods indicate that the field's potential value lies with the secondary-recovery program.
As the project provides new information for better characterizing the reservoir and revaluating the oil reserves, the design of real-options framework should allow for the review, adjustment, and revaluation of the staged field development plan, so that management could make better decisions as to abandoning, expanding, or scaling back the development.
Black-Scholes calculation
The Black-Scholes options pricing equation for computing an approximate call options value is a convenient way to obtain the options value of the Guando waterflood development. In the equation, the annual volatility is the most difficult parameter to derive and verify.7 For this example, the volatility used is the 33% annual standard deviation of EVs calculated from the decision tree analysis (Fig. 5).
A simulation is the best way to compute the volatility and other statistics for a project. But because of the number of scenarios defined in this project, this analysis would require a complex simulation model. Therefore, this analysis adopted the simpler derived value as an approximation. This value is influenced only by the possible outcomes included in the decision tree and the moderate correlation between the associated cash flows.
Sensitivity analysis can establish the impact of variations in the volatility value.
Another key parameter in the Black-Scholes equation is the premium or exercise price (EX). One can equate the capital investment associated with the pilot waterflood with the premium associated with a call option. This is the premium that must be paid to participate in the potentially beneficial, but not guaranteed, outcomes (for example proving up probable and possible reserves) that might result from the waterflood.
The weighted average NPV of all possible outcomes needs to be large enough to justify the initial investment (premium), after taking into account the uncertainties in the plan. One can equate the premium to the average capital cost of the waterflood outcomes. From Fig. 5, $136 million is the mean PV of the capital investment, including the waterflood outcomes.
Because Ecopetrol has to provide 50% of that capital investment, the premium value for the waterflood option is $136 million less the cost of the primary recovery of proved reserves (which is $92.4 million) multiplied by 50%. This equals $21.8 million.
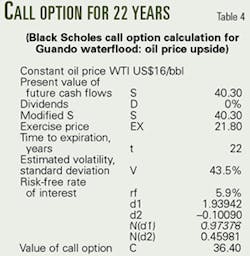
The input parameters for a simple Black-Scholes calculation for the calculated call value, shown in Table 3, are as follows:
- Volatility (standard deviation per year) = 33% (calculated for the first year).
- Risk free interest rate = 5.9%.
- Time period of option = 2 years (until Decision 2 - infill waterflood program).
- Dividends = 0% (expenditures for the project already are subtracted from cash inflows).
- PV of future cash flows = $40.3 million (from Table 1 and Fig. 5).
This calculated option value (premium/exercise price) of $21.2 million approximates the value associated with only the secondary recovery (waterflood) components of the field development. This can be considered as the premium value to Ecopetrol for maintaining a right of access to the Guando field development and obtaining the benefits of the probable reserves should they materialize.
The option value is close to the exercise price or premium paid by Ecopetrol for the right to participate in the option. Hence, addition of this option value to the proven reserves NPV represents a more realistic value of the field to Ecopetrol.
The value of the proved reserves incorporating primary recovery only at an oil price of $16/bbl is –$12.625 million (Table 1, selected pipeline option), suggesting a $9.08 million combined proved asset value plus option value. This value exceeds Ecopetrol's sole-risk $1.8 million value (Table 1) and enhances a positive decision to enter into the deal.
Sensitivity analysis associated with the volatility value used in the calculation indicates a call value of $20.9 for V = 10% and $26.5 for V = 90%. If the PV of future values is increased to $50 and $100 million, the call value is $30.7 and $80.6 million respectively. If the PV of future values is decreased to $30 and $10 million, the call value is $11.6 and $0.2 million respectively.
In the Guando case, the Black-Scholes options calculation complements the expected value calculations derived from the decision-tree analysis by placing an alternative value on the uncertain outcomes. The static decision tree assigns probabilities to a range of outcomes most of which will not occur.
The subjectivity associated with the assignment of probabilities is a weakness in such risked valuations. An alternative valuation, however, can be derived for the options component of the decision tree using options valuation equations, such as Black Scholes, that are based on sensitivity analysis and an assessment of volatility using the standard deviation of the decision tree expected values.
The options value and the expected value from the decision tree bracket the risked value associated with the flexibility of participating in the project uncertainty. That uncertainty will be resolved, at least partially, within a specified time period after which a decision is necessary to either exercise the option (in this case Decision 2 to drill the infill waterflood program) or relinquish it.
One can make the options calculation, with the Black-Scholes equation, very quickly with minimum effort because the assumptions of the equation are not violated, particularly the fact that volatility remains constant during the first 2 years of the pilot waterflood. It is the authors' view, however, that it is important to initially frame and evaluate a staged project and the optionality it contains in terms of a decision tree. This tree will highlight the potential outcomes at future decision points rather than simply relying on a numerical derivation of its options value.
For more complex projects, the simple European call Black-Scholes valuation often is inadequate to cover all aspects of optionality involved. The combination of decision trees and simulation are the best way for calculating the multitude of options that characterize the industry.
These analyses involve more complex numerical calculations but provide more appropriate approximations for establishing option values. The Guando example merely scratches the surface of the real options approach but highlights the need for incorporating an options methodology into the valuation of staged project.
Oil price uncertainty
It is important not to lose sight of the potential upside value associated with periods when oil price exceeds the base-case assumptions. Substituting 2004 oil prices into the Guando model makes it very profitable.
Ecopetrol used a conservative $16/bbl flat base-case oil price over the project life. This is less than historical $17.10/bbl average in real terms for the period 1985 to 2001 and the long run $19/bbl marginal crude cost for non-OPEC crude.
Ecopetrol could expect some oil price upside without forgetting that it is also possible that oil prices will be lower than the base case, in which case, the losses may offset much of the potential gains from high prices.
The question is how should this upside be valued? Oil can have a very wide range of future values. The long run annual average standard deviation for oil price is about 43.5%.
The best history matches of oil price fluctuations during recent decades have used a continuous mean-reverting price model with jumps. In this match, random abnormal information periodically generates discrete jumps of random size up and down.8 These forecasts can be used to model oil price volatility. But a simpler alternative is to use the Black-Scholes equation to approximate the positive gains associated with upside oil prices.
Table 4 shows the results of substituting the 22-field production life for time and the 43.5% for the expected long-run oil price volatility into the Black-Scholes model used in Table 3. This real-options upside price approximation assumes that a call option is effective every time that oil is sold during the production life of the field and that the long-run price volatility acts to expose the base-case PV to higher oil prices without penalizing them for lower (than base case) prices.
The call value calculates a $36.4 million gain in excess of the base-case NPV calculated previously. Sensitivity analysis yields call values of $34.1 million if volatility is reduced to 10% and $39.8 million if volatility is increased to 90%.
Given this result, the value of the Guando asset to Ecopetrol including oil price upside potential can be estimated as:
Upside asset value = $9.08 million + $36.4 million = $45.48 million.
Incorporating flexibility
If the Guando pilot waterflood is successful, Ecopetrol and its partners have the option to drill additional wells, increase injected water, increase oil production, increase ultimate recovery, and lengthen the exposure time to potentially higher oil prices than incorporated in conservative base-case assumptions.
If the pilot fails, Ecopetrol can exercise an option to cease further development drilling, minimizing subsequent losses.
This options approach to valuation increases the value of the Guando project compared to conventional DCF analysis because it includes the participant exposure to potential gains that may materialize from exercising the options while reducing potential losses. It also identifies the potential incremental values associated with the more uncertain categories of reserves.
More important, perhaps, is the ultimate valuations derived in the methodology of framing project alternatives and decisions in the context of a series of nested options. Thinking in terms of optionality, in itself, can lead to more meaningful and comprehensive evaluations of the complex decisions often associated with upstream oil and gas projects.
Acknowledgments
The authors express their gratitude to Ecopetrol and its partners in the Guando field for their approval to publish the information and analysis contained in this article.
References
1. Black, F., and Scholes, M., "The Pricing of Options and Corporate Liabilities," Journal of Political Economy, Vol. 81 (1973), p. 637.
2. Merton, R.C., "Theory of Rational Option Pricing," Bell Journal of Economics and Management Science, Vol. 4 (1973), p. 141.
3. Copeland, T., and Antikarov, V., Real Options: a Practitioner's Guide, New York: Texere LLC, 2001.
4. Chorn, L., and Sharma, A., "Project Valuation: Progressing from Certainty through Passive Uncertainty to Active Project Management," SPE Paper No. 77585, SPE Annual Technical Conference and Exhibition, San Antonio, Sept. 22-Oct. 2, 2002.
5. Miller, K., and Waller, G., "Scenarios, Real Options and Integrated Risk Management," Long Range Planning, 2003, p. 36.
6. Rutherford, S., "Deep Water Real Options Valuation: Waiting for Technology," SPE Paper No. 77584, SPE Annual Technical Conference and Exhibition, San Antonio, Sept. 22-Oct. 2, 2002.
7. Van Horne, J., Financial Management & Policy, 12th Edition, Sydney: Prentice Hall, 2002.
8. Dias, M.A.G., Real Options in Upstream Petroleum: Overview of Models and Applications, http://www. puc-rio.br/marco.ind/, November 2001.
The authors
Oscar Bravo ([email protected]) works within the corporate and risk planning division of Ecopetrol. He has 17 years of oil and gas experience with Ecopetrol as a petroleum engineer, project designer, and analyst. Since 2002, he has also taught courses on decision and risk analysis as a visiting professor at Universidad de los Andes, Bogota. Currently, Bravo holds an MBA from University of Illinois
David Wood ([email protected]) is an international oil and gas consultant specializing in the integration of technical, economic, risk and strategy evaluation, and training. He has more than 25 years of industry experience. Wood holds a PhD from Imperial College and has worked with major and independent operating companies.
David Wood writes in detail about related subjects in four executive reports available for purchase through the Online Research Center of Oil & Gas Journal Online. For a list of titles and descriptions, go to www.ogjonline.com, click "Online Research Center" on the left navigation bar, then click the link under "OGJ Executive Reports."