Understanding draft limitations in fired heaters
Norman P. Lieberman
Process Improvement Engineering
Metairie, La.
A South American refinery's experience with a draft-limited fired heater emphasizes the pivotal role process engineers play in finding solutions to problems that occur in plant equipment.
To be effective, the engineer must quickly call upon elementary engineering principles, conduct thorough field investigations, and communicate with equipment operators.
An example of this approach to solving operational issues occurred at Ecopetrol SA's 165,000-b/d refinery in Cartagena, Colombia, where a process engineer's request for proofreading help initiated a lesson for anyone involved in running an industrial process plant.
The steps taken to resolve the heater's draft deficiency involved hands-on inspection of field equipment and operating conditions alongside basic calculations to determine available draft in the heater's stack.
The solution enabled the refinery to avert costs and delays associated with an alternative proposal to contract computer software simulations. More importantly, the solution safeguarded lives that could have been lost during the wait for simulation results.
Heater draft limit
"Que pasa, mi amigo, Pedro?"
"Señor Norm, por favor, could you look over this letter to Foster Wheeler Corp. in New York to make sure it is all correct, all in proper English?"
The letter described a flame impingement problem on the crude unit's fired heater, suggesting the heater was draft limited. For a fee of $10,000, the letter authorized Foster Wheeler to use appropriate computer simulation software to help calculate the draft of the heater's stack and transmit those results back to the refinery within 30 days.
Given the cost and distant deadline of the proposed arrangement, the author pressed for additional details, at which point the young engineer revealed:
• The stack was very tall (about 50 m high).
• The stack damper was wide open.
• When refinery personnel opened the burners' air registers, flue gas was blowing out of the furnace sight ports because of positive pressure beneath the bottom row of convective tubes.
To make matters worse, the heater was burning fuel oil with 3% sulfur content, which meant the flue gas blowing from those sight ports contained toxic SO2.
Alarmed by the dangerous and potentially deadly situation created by the ongoing SO2 release, the author agreed that (1) positive pressure indeed existed at the top of the furnace's radiant section, and (2) the next step required a trip to the plant.
The office is a fine place to establish that a problem requires corrective action, but talking alone is unlikely to lead to the proper one.
A red balloon
During the drive out to the Cartagena plant, the author reflected on how little he'd progressed from childhood in the sense that the tests he runs in process plants today are nearly the same as those he carried out as a child to understand the workings of the world around him.
While the voice calling for him to stop his work to eat dinner may now be that of his wife instead of his mother, the drive to apply basic principles to complex questions is the same as it was during his childhood in New York City.
The long ride to the refinery afforded the author an opportunity to share with the young engineer a relevant experiment from his childhood to help simplify the problem that awaited them.
The author's childhood experiment involved a test to determine how many small lead fishing weights a large red helium-filled balloon could lift so that it would remain suspended in his bedroom. To conduct the experiment, the author only had to apply principles and calculations that he'd learned in school.
The first step involved determining the density of helium inside the balloon. To do this required knowing the molecular weight of helium (4 lb), the molecular weight of air (29 lb), and the density of air (0.076 lb/cu ft) at sea level and 70° F., the same conditions as the author's room.
After calculating the density of helium inside the balloon as 0.010 lb/cu ft (Equation 1), the author was able to calculate the difference of density between the helium inside and air outside the balloon as 0.066 lb/cu ft (Equation 2), as well as the volume of the round balloon as 3 cu ft (Equation 3).
With these determinations, the lifting force of the balloon was calculated as 0.20 lb (Equation 4). Knowing 16 oz. are in 1 lb., the author concluded that lift on the balloon would be 3.2 oz (Equation 5).
To verify the theoretical lift force of the balloon, the author used his father's postal scale to measure 3.2 oz of paper, of which the balloon disappointingly could only lift 2.5 oz.
In reviewing the experiment, the author realized he'd neglected to consider the weight of the balloon itself. With both theoretical and actual lift force known, the author was able to calculate the balloon's weight at 0.7 oz (Equation 6).
Temperature effect on lift
Helium is expensive, and hydrogen is dangerous due to its combustibility. So if you want to go on a balloon ride, the balloon is going to be lifted by hot air.
A balloon 40 ft in diameter will have a volume of 32,000 cu ft (Equation 7).
Ambient temperature is 70° F. The hot air inside the giant balloon has been heated to 300° F. The elevated temperature forces the molecules of air away from each other, making the air less dense in proportion to its temperature. The lower density is not in proportion to temperature measured in °F., however, but in proportion to temperature in Rankine (°R). To convert from °F. to °R., add 460 to the °F. temperature (°F. + 460 = °R.).
In our example of the giant balloon, the ambient air temperature would be 530° R. (Equation 8) and the hot air inside the balloon, 760° R. (Equation 9).
With the density of air at 70° F. equivalent to 0.076 lb/cu ft, the density of the 300° F. (760° R.) hot air inside the giant balloon equals 0.053 lb/cu ft (Equation 10). The density difference between the hot (300° F.) air inside and cool (70° F.) air outside of the giant balloon would be 0.023 lb/cu ft (Equation 11). Having already established a volume of 32,000 cu ft for the giant sphere, the balloon would be able to lift 740 lb (Equation 12).
Stack draft
A tall stack can develop a very strong sucking force. Let's say the stack's draft is 2 in. H2O (meaning pressure outside the stack is 2 in. H2O higher than pressure inside the stack). Let's also say there is a metal plate measuring 2 ft × 2 ft to be pulled off the stack's bottom. How much force, in pounds, would one have to use to pull off the plate?
First, we calculate the area of the plate as 4 sq ft (Equation 13), or-since we know there are 144 sq in. in 1 sq ft-576 sq in. (Equation 14).
Over the surface of this plate, there is a force of atmospheric pressure equal to 2 in. H2O pushing on the plate, which we can calculate as 1,152 cu in. (Equation 15).
Since 1 cu in. H2O weighs 0.58 oz, we can determine the force required to pull off the plate would be 664 oz (Equation 16), or 42 lb (Equation 17).
The author encountered this problem in 1980 at Amoco Oil Co.'s Texas City, Tex., refinery where, while wearing a Scott Air-Pak, he had to pull off a manway cover on a reactor that was 150 ft high and full of hot flue gas from burning sulfur residue.
Stack height effect
Draft in a stack is not caused by combustion. Also, as the molecular weight of the flue gas is rather close to air, its effect is neglected. And while wind blowing across the top of a stack occasionally contributes to draft, its effect is generally ignored when calculating draft since it's not always windy.
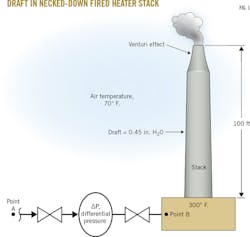
You may have seen on certain stacks that the top end of the stack is necked-down (Fig. 1). This is done to slightly increase the draft. It's called the Venturi effect, which will be discussed later.
Major factors contributing to draft in a stack include:
• Height of the stack.
• Temperature of the flue gas.
• Ambient air temperature.
Let's say a stack is 100 ft high. The ambient air temperature is 70° F., and the temperature of gas inside the stack is 300° F. The molecular weight of the gas inside the stack is pretty close to air. If you refer back to the example of the giant hot-air balloon calculation, the density difference between the cool (70° F.) ambient air and the heated (300° F.) air inside the balloon was 0.023 lb/cu ft. This density difference applies to the entire 100-ft height of the stack so that the effect is similar to that inside the balloon, where cold, denser air pushes up the lighter, hotter air. In other words, the 100-ft column of colder air forces up the 100-ft column of hotter air inside the stack.
This pressure difference is called draft. It is a result of the density difference between hot flue gas in the heater stack and the ambient air outside multiplied by the 100-ft height of the stack, which in this instance, is calculated as 2.3 lb/sq ft (Equation 18).
Anyone who has worked on a process heater knows draft is never expressed in lb/sq ft, but in inches of H2O. Converting lb/sq ft to in. H2O requires a two-step calculation that involves first converting draft in lb/sq ft into psi by dividing stack draft by 144 sq in./sq ft, which works out to be 0.016 psi. (Equation 19).
But how do you convert from psi to in. H2O? If you fill a glass tube with cool 60° F. water to a height of 28 in., and then place a pressure gauge at the bottom of the tube, your gauge will read 1.0 psi (Fig. 2). This means that to convert from psi to in. H2O, multiply the psi value by 28. The draft in our 100-ft high stack full of 300° F. stationary air, then, is 0.45 in. H2O (Equation 20).
Don't we need fire to create draft?
What we require to create draft in a stack is heat to warm the air from 70° F. to 300° F. The pressure at the top of the stack is ambient.
If we heat air inside the stack with an electric heating coil and cap the stack's top to prevent flow, we would still measure the inside pressure at the bottom of the stack to be 0.45 in. H2O lower than ambient air pressure outside of the stack.
As the gas inside the stack gets hotter and less dense, draft increases. As the air outside the stack cools and becomes denser, draft also increases.
The author has omitted three elements from this analysis because of their minimal impact on draft. These include:
• The frictional losses of flue gases in the stack, as stacks are made fat enough for friction to not play a role (e.g., velocities less than 50 fps).
• The molecular weight difference between air and flue gas.
• Wind blowing across the top of the stack.
In situations where wind is a factor, however, it can be a significant problem, especially when we try to save on energy costs by minimizing excess combustion air in a fired heater.
The author observed in a Wyoming refinery that a 30-mph gust of wind will cause a sudden draft increase of slightly more than 0.1 in. H2O, or about 20%. This will increase the combustion air flow into a fired heater by around 10%, which in the event of a heater running with 2% excess O2 in the stack means the excess O2 will suddenly increase to about 4%.
Alternatively, if you're running a heater at 2% excess O2 and the 30-mph wind stops, the heater will be running in an air-deficient mode, causing possible accumulation of explosive gases in the convective section. If this type of situation occurred with fuel gas on automatic temperature control, the consequence could be a heater explosion.
Venturi effect
During the 30-min. trek to the refinery, past banana groves and hillsides covered by withered corn stalks, the author was reminded of and shared with the young engineer an anecdote. While driving down a gravel road in southern India, the author passed a small plant boiling down sugar cane juices to produce molasses. He noticed that the 20-in. diameter of the plant's brick boiler stack narrowed to perhaps 6 in. near the stack's top.
The author reasoned that this reduction in the cross-sectional area of the stack would increase the velocity of flue gases exiting the top of the boiler's stack, and that such an increase in flue-gas velocity would decrease pressure at the top of the stack. Theoretically, this should result in a slight draft increase in the boiler, located at the base of the stack, to help draw in more combustion air.
To confirm the theory, the author stopped to ask two older gentlemen working around the juice boiler why they thought the top of their stack was narrower than the bottom. He suggested the narrowing was an application of the Venturi effect
The gentlemen responded that the narrowing was not done to honor this Mr. Venturi, as they'd never heard of any such person. Rather, it was done to honor a tradition handed down from many generations of ancestors, holding that narrowing the top section of the stack helps the boiler work harder.
This was another basic engineering principle to consider before arriving at the plant to begin the real work of field observations and data collection.
Solving the problem
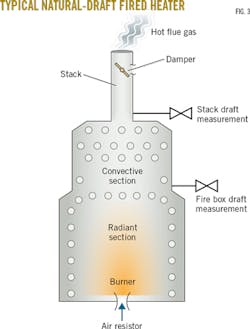
On site at Cartagena, the crude heater showed multiple signs that it was operating in a draft-limited situation (Fig. 3):
• The burner air registers were mostly closed.
• Yellow flames were licking up against the radiant-section wall tubes.
• Wisps of white (e.g., SO2) flue gas were escaping from leaks just below the convective section.
• Increasing the fuel flow caused the heater outlet temperature to drop-a sure sign of lack of combustion air.
After looking up at the stack damper and seeing the arrow pointing straight up to indicate the damper was wide open, the author began a series of steps to gather data to understand and resolve the problem.
Step 1 involved using a bottle of blue-colored water and 4 ft of clear plastic tubing to measure the draft above the convective-section tube bank. Results indicated a draft of about 0.3 in. H2O (meaning that's how high the blue water was sucked up into the tubing by the slight vacuum at the stack's base).
In Step 2, the author calculated the draft that should have been generated by the stack using the flue gas temperature and stack height, which yielded a theoretical draft of 0.9 in. H2O (Equations 18-20).
Step 3 involved calculating the draft loss-or pressure drop of flue gas-through the damper by subtracting the draft above the convective-section tube bank (0.3 in. H2O) from the stack's theoretical draft availability (0.9 in. H2O) to determine a draft loss of 0.6 in. H2O (0.9 - 0.3 = 0.6 in. H2O).
This calculation was completed in less than 30 days and at a truly unbeatable cost vs. the proposed computer software simulation, especially since the author did not have to remove his gloves to complete it.
One question still remained, however: How could a wide-open stack damper be causing a pressure drop equivalent to 65% of the stack's height?
In a fourth step to help answer the question, Pedro, while observing the blue water level in the plastic tube, slowly closed the stack damper until the damper-position arrow moved from its vertical, straight-up position to an inclined 45° position. The draft-which had been reading a rock-steady 0.3 in. H20-remained unchanged!
Having experienced this situation once before in a New Jersey refinery, the author had a crane with a basket brought to the stack. For the fifth and final step of field work, Pedro-armed with a 30-in. pipe wrench-stepped into the basket and was lifted to the stack's damper shaft.
Once in place, he twisted open the damper shaft until the blue water in the plastic tube rose to 0.9 in. H2O. At this point, the author confirmed the stack damper now was truly wide open.
The answer to this mysteriously massive pressure drop at the stack, then, was simple. The stack-damper chain operator was moving the damper-position indicator arrow, but not the stack damper itself.
With this issue corrected, the crude heater flames retreated from the fire box walls; the burner air registers could be opened without risk of blowing deadly SO2-laden flue gas out of the heater's radiant-section roof; and the fuel gas flow rate was safely increased.
GENERAL INTRODUCTION
Geared to young and seasoned professionals alike, "Beyond back-to-basics: Process principles and concepts" is a new series of articles designed to present a straightforward approach to mastering the principles and concepts all process engineers should be able to apply without the need of a computer.
While simulations and models are useful for examining long-term operational issues, they cannot replace the dimension of human logic and reason required when tackling the array of complex-and sometimes life-threatening-situations that occur in process plants.
Using experiences from the author's more than 50-year career in the process industry, articles in the series will provide approaches to understanding core process concepts in ways that will equip the engineer to walk out of an office, into a plant, and directly resolve process deficiencies via small operational changes or simple retrofits.
The author
Norman P. Lieberman ([email protected]) is a chemical engineer with 53-years' experience in process plant operation, design, and field troubleshooting. He served as a process engineer, operations supervisor, technical service manager, and plant manager in US refineries until 1985. An independent consultant, he has taught 800 seminars on troubleshooting refinery process problems to 19,000 engineers and operators. An author of nine textbooks on process problems and operations, he holds a BS (1964) from Cooper Union, New York, NY, and an MS (1965) from Purdue University, West Lafayette, Ind., in chemical engineering.