BEYOND BACK-TO-BASICS: PROCESS PRINCIPLES AND CONCEPTS-3: Maintaining seal-flush pressure in centrifugal pumps
Norman P. Lieberman
Process Improvement Engineering
Metairie, La.
Centrifugal pumps are the most common pumps in a process plant. Despite their pivotal role in operations, however, they are often the plant's least understood and most inefficiently operated equipment.
Operators' fundamental understanding of how pump systems work will determine how much time and money a refinery spends on keeping a unit's pumps-often numbering more than 100-in working order. Many operators, however, only learn about pump operations once on site by trial and error from fellow operators who may not know what they're talking about. The knowledge gap can be considerable, ultimately translating to the higher costs associated with unnecessary maintenance, downtime, and replacement of equipment.
As I learned as a field troubleshooting engineer, a simple conversation between a process engineer and unit operator about how centrifugal pumps work can lead to large and sometimes unexpected cost recoveries for the operating company by helping maximize the efficiency of existing operations.
Adjusting seal-flush pressure
"Donald, I've told you before not to use 100 psi on the seal flush, that 20 psi is enough."
"But, sir, that's too low. The pump-discharge pressure is 80 psi. The seal-flush pressure needs to be above the discharge pressure by about 20 lb."
"That's completely wrong. The pump's seal-flush pressure must be a bit higher than the suction pressure, not the discharge pressure, especially since the pump is in reduced crude service and the flushing fluid to the seal is diesel. You're losing a lot of valuable diesel product to the reduced crude."
"Really, Mr. Norm? It can't be losing a lot, can it?"
"It depends on the mechanical seal's design," I explained, sharing the following rules of thumb to consider when determining seal-flush flow rates:
• For older pumps with a component seal, about 3-4 gpm per inch of shaft diameter is needed when the pump is running, half that amount when the pump is idle, and twice that amount if there is both an inboard and outboard seal.
• For more modern pumps with cartridge seals, one-third the amount of seal flush is consumed as when running older pumps with a component seal.
• If the seal flush pressure exceeds its design pressure by a large amount because it's running above the discharge pressure (vs. just above the suction pressure), the amount of seal flush may increase in proportion to seal flush flow.
Seal flush flow ≈ (Pseal ÷ Psuction)0.5, where Pseal = seal oil pressure downstream of the seal-flow adjustment valve and Psuction = pump-suction pressure downstream of the pump's suction strainer.
"Mr. Norm, what you said only makes sense if the pressure inside the entire pump case is the suction pressure rather than pump-discharge pressure. But the pressure of liquid inside the pump case is certainly the discharge pressure, because the liquid has been pressured-up by the pump impeller."
"Donald, you'd be correct for a positive-displacement pump, but it's not right for a centrifugal pump. Like 95% of the pumps in our plant, this pump is an ordinary centrifugal pump, where the function of the impeller isn't to increase the process-liquid pressure, but to accelerate the flow."
"I thought I understood how pumps worked, but now I'm confused," Donald confessed. "Could you explain this to me?"
So I did, using the principles I'd applied as a kid in Brooklyn, NY, to help answer the same question.
Velocity, head, pressure
When I was 12 years old, I'd been told the water pressure in our bathroom was 40 psig. Never one to trust hearsay, I devised an experiment. I took our bathroom scale into the backyard, adjusted the nozzle of the garden hose to ensure the biggest water pressure possible, and directed the jet straight down onto the scale.
Much to my disappointment, the scale reading increased only to about 6 lb rather than the 40-lb measurement I'd expected to see. On closer observation, I noticed that the jet of water was concentrated on the scale in a circle with a diameter of only 0.5 in., which I converted to an area of 0.2 sq in.
A = π x (d2 ÷ 4), where A = area of a circle in sq in., π = 3.14, and d = diameter of the circle in inches.
Next, I divided the 6-lb reading on the scale by the circle's 0.2-sq in. surface area to arrive at an adjusted water pressure of 30 psi. I figured that the 10-psi discrepancy between my experiment and the bathroom's water pressure of 40 psig must be due to losses occurring during the water's 1-mile journey to my house from the tower on Benson Ave.
While I could understand that 10-psi loss, what I found confusing was that the water flowing from the garden hose nozzle was at atmospheric pressure, or zero psig, not 40 or 30 psig. What, then, was the cause of that 30-psi pressure that I measured on my bathroom scale?
Converting velocity to flowing pressure
Nearly three centuries ago in Switzerland, Daniel Bernoulli observed energy could appear in several forms, including:
• Heat (thermal energy).
• Velocity (kinetic energy).
• Head (potential energy).
• Pressure (effect of gravity).
• Electricity.
Directing a jet of water from a garden hose straight up converts the high velocity (kinetic energy) of the water into feet of head (potential energy). At sea level, we can calculate this using the following equation: DH = 0.178 × V2, where DH = water height measured in inches, V = water velocity in fps, and 0.178 = the theoretical factor for converting velocity (kinetic energy) of water to inches of water head (potential energy).
If I were to shoot water out of my garden hose at 30 fps straight into the sky above me, the stream should reach about 160 in., or 13.5 ft (not accounting for frictional losses, of course).
Pump impeller function
"Mr. Norm, you've drifted off the subject of pump impellers."
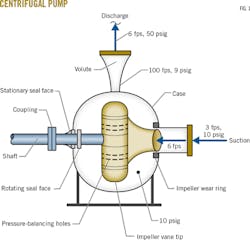
"Not really, Donald," I said, moving our discussion to a more hands-on look at the pump (Fig. 1).
"A typical suction-piping velocity might be 3 fps before the liquid flows into the eye of the pump's impeller and accelerates, let's say, to 6 fps. That flow acceleration to 6 fps from 3 fps requires energy."
"Does that acceleration energy come from the pump's impeller?"
"No, Donald, it comes from the potential energy of the liquid, or from the head of liquid."
"Is that what engineers call the required net positive suction head (NPSH) of the pump?"
"It's exactly that," I said.
"And if the required NPSH isn't smaller than the head of liquid available in the vessel, then I need to raise the vessel liquid level, right? Otherwise, my pump's going to cavitate?"
"You got it, Donald," I said. "You'll tear up the pump's mechanical seal due to vibration."
"This is interesting, Mr. Norm. So what happens to the liquid after it flows into the eye of the impeller?"
"The liquid spins around inside the impeller, where it accelerates from 6 fps to 100 fps as it discharges from the impeller's vane tip (Fig. 1)."
"But where does that energy to accelerate the liquid come from? Also from the available NPSH?"
"No, it comes from the electric motor, or the steam turbine, spinning the impeller."
Donald paused for a moment to consider this, and sensing his confusion, I explained the process in more detail.
According to Bernoulli, electricity-a form of energy-can be converted to kinetic energy, which is what's happening inside the pump's spinning impeller.
The pressure of the liquid discharged from the impeller is slightly lower than the pump suction pressure. The impeller discharge pressure is the pressure inside the entire pump case. To ensure the pump's seal doesn't experience pressure much above the pump suction pressure, there are pressure-balancing holes drilled through the impeller, which I pointed out to Donald.
"Yeah, I've seen those holes before. Jerry told me they were there to equalize pressure on both sides of the impeller. Is that right?"
"Yes, Donald, Jerry is correct. But that pressure he's referring to is the pump-suction pressure, not the discharge."
"Mr. Norm, I'm still confused. None of this makes any sense. How does the pump-discharge pressure increase from the 10 psig suction to the 100-psig discharge?"
Converting velocity to head
To explain the concept, I had Donald look at the discharge nozzle of an unflanged pump.
"Do you see how the discharge flange is 6 in., but the opening down inside the pump case is a lot smaller?"
"Yes, sir, it looks like it's about a 1.5-in. opening."
"It follows then (from Fig.1), that the velocity at the 6-in. discharge flange has dropped from 100 fps down to 6 fps (100 fps x [1.5 ÷ 6]2 = 6 fps). The reduction in velocity has been converted into…"
"Hey, I think I get it, Mr. Norm!" Donald interjected with excitement.
"Whoa, Donald, that's great. Just to make sure, though, go ahead and explain it to me."
"It's just like a roller coaster car slowing down as it goes uphill. The speed of the car is converted to elevation, like what you call feet of head or what that Swiss guy Bernoulli calls potential energy. But that doesn't happen until the liquid's out of the pump itself, which is why the seal-flush pressure only needs to be a little bit higher than the pump's suction pressure."
"Okay," I said. "Keep going."
"The discharge pressure really doesn't affect the pressure that the pump's mechanical seal has to hold, but even if the seal-flush pressure did build up a bit behind the impeller, that pressure would bleed itself back to the pump suction through those pressure-balancing holes drilled in the back side of the impeller. Yeah, I got it!"
And he did, for the most part. But Donald's questions didn't end here.
Head, discharge pressure
"Mr. Norm, you keep talking about head, but that doesn't mean anything to me. As an operator, I only see pressure. Doesn't the centrifugal pump create a certain amount of discharge pressure?"
"Well, yes and no, Donald."
"Could you make up your mind? Does a centrifugal pump increase the pressure of the liquid it's pumping?"
"A centrifugal pump, which is pumping a nonviscous product, develops a certain amount of feet of head at a given volume of flow, regardless of the density or specific gravity of the liquid pumped," I said. "To be more clear..."
"Mr. Norm, you couldn't be less clear," Donald said. "But go ahead. Talk slowly and I'll listen."
"As I was saying, Donald, since we know that water has a specific gravity of 1.0, and that 1.0 psi of pressure equals 2.31 ft of water, we can use the following equation to convert from feet of head-which is what the pump creates-to pressure:" DP = (DH × sp gr) ÷ 2.31, where DP = the increase in discharge pressure over suction pressure in psi, DH = increase in feet of head developed by the pump in ft, and sp gr = specific gravity (density) of liquid at flowing temperature relative to the density of cold water at 60° F.
"So a pump that's pumping diesel will create more discharge pressure than one pumping naphtha because diesel is denser than naphtha?"
"Correct, Donald."
"Okay, I get the specific gravity idea," Donald said. "But how about the nonviscous stuff? What's all that mean?"
"Well, 90%+ of the liquid we handle in a refinery is low-viscosity material, meaning its less than 50 cst. In our plant, the only high-viscosity stuff is cold Venezuelan crude, or cool slop wax from the vacuum tower. We'd handle anything that has a viscosity of more than 50-100 cst with a positive displacement pump, not a centrifugal pump."
"Let's just stick with the centrifugal pump for now," Donald said. "You mentioned earlier about feet of head at a given volume of flow, and I'm not sure I get what you mean. Could you walk me through it?"
Pump curve
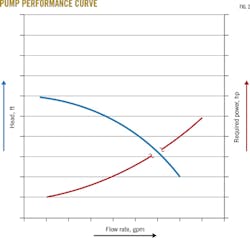
"A centrifugal pump operates on a performance curve (Fig. 2). The head depends on the volume of liquid. So whether you're pumping water with 1.00 sp gr or gasoline with 0.75 sp gr, a pump will produce the same feet of head as long as the flow is constant."
"Okay," Donald said. "But how about that horsepower curve? I guess that's the same for water and gasoline also?"
"I know it's confusing, but no," I explained. "The motor horsepower-or the amount of amps the motor will pull-is a linear function of the specific gravity. If the specific gravity increases by 20%, so will the motor amps. Manufacturers develop pump curves using water in a test rig. Even though a pump may be designed for diesel with a 0.85 sp gr, the horsepower shown on the right-hand vertical axis of the pump curve is likely the required horsepower for water."
"Man, that's really confusing," Donald said. "Even so, Mr. Norm, I'm glad you clarified it for me because it explains why P-403 trips off on high-motor amps when I switch from water to caustic, unless I throttle back on its discharge first."
"Right, Donald, the specific gravity of the water is 1.00, while the caustic has a 1.20 sp gr. At the larger specific gravity, you're going to be limited by motor horsepower, not the pump's capacity."
Positive displacement pumps
"Mr. Norm, it's near the end of my shift, but before I head to the gate, I have one more question. Out in the tank field, we have a crude pump that I've been told is different from all the centrifugal pumps on our unit. It looks the same as our centrifugal pumps. What's the difference?"
"I get confused by this also, Donald. While they look the same, that pump in the tank field is a positive displacement pump."
"You mentioned that type of pump earlier. So what's the difference?"
"An important one," I said. "As the performance curve shows, centrifugal pumps develop the same feet of head for a particular flow rate. Positive displacement pumps, however, don't run on a curve. Instead, they generate as much head or discharge pressure as they need to overcome the pressure of the system into which they're pumping."
"Translation, Mr. Norm?"
"Think of it this way, Donald. If the pump needs to push 100,000 b/d of crude into a tank, its discharge pressure might be just 25 psig. If the pump needs to push 100,000 b/d of crude into your crude unit, its discharge pressure could be 150 psig."
Seal-oil flow to idle pumps
What began as my answer to Donald's question had evolved into a discussion about the fundamentals of centrifugal pump operations.
"Wow, Mr. Norm, that's a lot to take in, but it's the best explanation I've ever gotten, including from books, on how pumps actually work. I'm going to reset the seal-flush pressure just a bit above the pump's suction pressure on all my pumps tomorrow, just like you told me. By the way, does that go for the spare pumps we aren't running?"
"No, and I'm glad you asked," I said. "But now I have a question for you. Do you know why the answer's no?"
After a brief silence and with a slightly panicked look in his eyes, Donald shook his head from side to side.
"Donald," I said in a gruff voice. "I'm teasing you."
"Wow, Mr. Norm, you really had me going there for a second," Donald said, smiling now in relief.
"Actually, I'm only partly kidding because the answer is important," I said.
"Alright, Mr. Norm, why is the answer no?"
"Take your resid pumps, which use diesel for seal flush," I said. "When you shut the pump down, you wait a few minutes for the diesel oil to flush through the pump and then block the diesel seal flush in. Even though the pump isn't running, the seal-flush flow will still be around 60% of its flow when the pump was in operation. Every barrel of diesel you put into resid is costing the refinery about $10. Let's not waste seal flush on idled pumps."
"Man, they should have told me that when I was hired," Donald said. "I've been leaving the seal flush lined up to my idle pumps for years. Someone should've told us operators before not to do that. What a waste!"
"You're right, Donald, a big waste," I said. "But the important thing is that you know now. So walk in the light while there is light, my friend."
"Will do, Mr. Norm."
General Introduction
Geared to young and seasoned professionals alike, "Beyond back-to-basics: Process principles and concepts" is a new series of articles designed to present a straightforward approach to mastering the principles and concepts all process engineers should be able to apply without the need of a computer.
While simulations and models are useful for examining long-term operational issues, they cannot replace the dimension of human logic and reason required when tackling the array of complex-and sometimes life-threatening-situations that occur in process plants.
Using experiences from the author's more than 50-year career in the process industry, articles in the series will provide approaches to understanding core process concepts in ways that will equip the engineer to walk out of an office, into a plant, and directly resolve process deficiencies via small operational changes or simple retrofits.
This is the third article in the series.
Safety note
Autoignition is the temperature at which hydrocarbons can burn without a source of ignition. Except for hydrogen, the heavier a hydrocarbon is, the lower the temperature it requires to autoignite.
Gasoline has an autoignition temperature of 480° F. Asphalt, when spread over a porous surface like clothes, autoignites at 300° F. This is why a seal leak on heavy vacuum gas oil pumps is so dangerous.
It's much safer to get a sample of naphtha at 350° F. than vacuum resid at the same temperature.