Rotor vibration dynamic analysis helps detect compressor defects

Turbine dynamic-behavior analysis consists of studying vibration characteristics of the gas turbine rotor. Determining the rotor's energy allows analysis of dynamic behavior at nominal rotational speed within a limited range of several frequencies. Research sought to determine rotor response to dynamic excitation. Disturbances in mechanics are generated by vibrations either from outside systems such as adjacent machines, or from the gas turbine itself, such as residual unbalance, lack of lineage, or bearing degradation.

Shaft

The expression of the shaft's kinetic energy is an extension of the expression of the disk's kinetic energy. For an element with length, L, Equation 1 calculates kinetic energy.¹¹ Shaft deformation energy is calculated via deformation of a point on the shaft's straight section (Fig. 1) as expressed in Equation 2.

Equation 3 expresses the deformation,¹² while Equation 4 calculates deformation energy.

Unbalance response

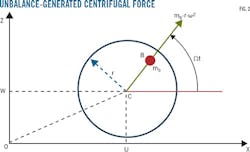
Unbalance is characterized by its kinetic energy, when mass mb is at point B in the disk's plane at distance d from its geometric center C. Equations 5 and 6 provide the unbalance coordinates in fixed coordinate system oxyz (Fig. 2). Equation 7 calculates unbalance kinetic energy. The term Ω2d2/2 is constant and will not intervene in the equations. The mass of the unbalance is negligible relative to the rotor mass and kinetic energy can be approximated as shown in Equation 8 by introducing generalized coordinates (Equation 9).

Bearings guide the rotating shaft in a stationary turbocharger. Radial load is weak and caused primarily by the unbalance, which may be reduced if necessary. A few major factors contribute to ball bearing damage:^13-18

• Superficial material fatigue resulting from the constraints-concentration effect produces flaking and cracking. This superficial fatigue can be aggravated by such other factors as insufficient lubrication, surface conditions, and shock.

• Contact wear, which can be compounded by oil contamination, bearing load, speed, and vibration,

• Contact corrosion.

• Heating, seizure.

Equations frequency

For a ball bearing with nb number of balls, rotating at shaft-rotation frequency f, a default such as stripe, flat, etc., differentiates the various rotating elements, the frequencies of which are defined in Equations 10-15, where d is the ball diameter, and φ the contact angle between the ball and raceway.

Equation 10 defines the frequencies related to default on each of the rotating elements for a defined unbalance. Equation 11 provides defects on the inner ring. Equation 12 accounts for modulation of the signal by frequency fc on inner-ring defects.

Equation 13 yields defects on the ball, with Equation 14 accounting for modulation of the signal by frequency.

Equation 15 provides fundamental cage frequency. Construction imperfections, assembly problems, or rotor operations lead to signal modulation.

Application results

Experimental results came from measurements taken on the rotor of gas turbine MS5002b, in service at Sonatrach's TRC Timzhert CC1 compressor station on the southern side of Hassi R'mel, Algeria. Researches gathered data from Bearing #1 and #4 in a vertical orientation and shaft rotation speed, ω, of 4,530 rpm.

The lack of information on the contact angle of the ball requires using equations based on testing more than 2,000 different types of bearings. Equations 10, 12, 14, and 15 give the frequencies for different bearing components. Equation 16 calculates shaft rotation frequency.

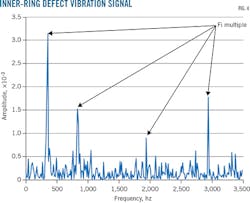
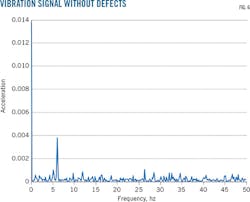
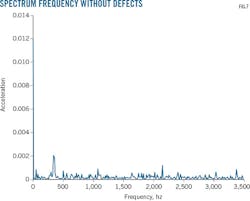
The measured values of the turbine at Bearings 1 and 4 present vibration defects in a vertical direction over 0-3,500 hz and 0-6,000 hz, respectively. Figs. 4-5 present the amplitude of the vibration signal as a function of its frequency. Fig. 4 shows an inner-ring bearing fault and Fig. 5 the vibration signal as a bearing failure due to a defect of the ball itself. Fig. 6 shows the vibration signal without a fault

These obtained results under actual conditions are presented to show the amplitude of the signal versus its frequency. The lifespan of the bearings depends on the load applied to the shaft, the rotational speed, and the force action point.

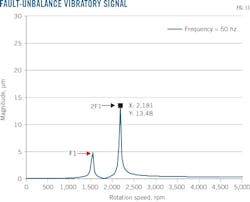
This kind of component appears when the shaft of the turbine operates under a bearing default explained by the presence of oscillations in the torque load and keeps the machine operating stably. These fluctuations occur at the same characteristic frequency of the defect.

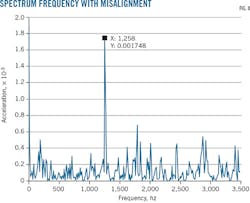
Figs. 7-8 show the envelope spectrum calculated for the different cases of operation in misalignment. The frequency signal of a misalignment defect appears as a peak amplitude with 2 or 3 times the rotor's rotation frequency. Fig. 7 shows the spectrum at the rotation frequency without defects. Figs. 8-9 show the spectrum at the rotation frequency with misalignment.

Figs 7-8 show spectral structure evolution successively when a fault is added. At 4,530 rpm and 75.5 hz, in a frequency range of 0-6,000 hz, a peak appears at the shaft rotation frequency characterizing the misalignment fault seen in Figs. 8-9.

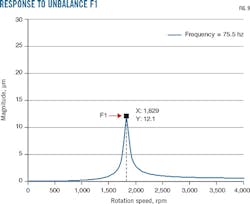
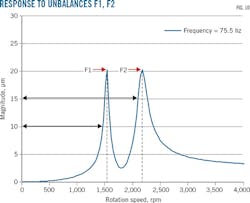
Balancing processing compensates for this poor distribution by adding or removing known masses at specific rotor locations. Additional work checked the system's capacity to address strong unbalances. Fig. 9 presents a test with two balancing speeds, designed to reduce all vibration levels at all rotor speeds. Displacement amplitude is increased in speed without balancing.

Fig. 10 shows rotational speed, including a peak at frequency F1 of 20 μm and a harmonic at (2 × F1 = F2) 35 hz, with an amplitude of 20 μm indicating an imbalance in the shaft.

Maximum amplitude identifies critical speed, with rotor displacements characteristic of sensitivity to a dominant unbalance mode. Fig. 11 shows the balancing rotational speeds' portion of vibration amplitude measured on the rotor as it accelerated toward critical speed

References

1. Arsalis, A., "Thermoeconomic modeling and parametric study of hybrid SOFC-gas turbine-steam turbine power plants ranging from 1.5 to 10 Mw," Journal of Power Sources, Vol. 181, No. 2, July 1, 2008, pp. 313-326.

2. Djaidir, B., Hafaifa, A., and Abdallah, K., "Performance control of gas turbines," Turbomachinery International, No. 6, November 2015, pp. 10-14.

3. Djaidir, B., Hafaifa, A., and Abdallah, K., "Monitoring Gas Turbines Using Speedtronic Mark VI Control Systems," Pipeline & Gas Journal, Vol. 242, No. 10, October 2015, pp. 48-86.

4. Combescure, D. and Lazarus, A., "Refined finite element modelling for the vibration analysis of large rotating machines: Application to the gas turbine modular helium reactor power conversion unit," Journal of Sound and Vibration, Vol. 318, Nos. 4-5, December 2008, pp. 1262-1280.

5. Ewins, D.J., "Control of vibration and resonance in aero engines and rotating machinery - An overview," International Journal of Pressure Vessels and Piping, Vol. 87, No. 9, September 2010, pp. 504-510.

6. Greco, D., Blanc, P., Aubry, E., and Vaclavik, I., "Active vibration control of flexible materials found within printing machines," Journal of Sound and Vibration, Vol. 300, No. 3-5, March 2007, pp. 831-846.

7. Cheddie, D.R. and Murray, R., "Thermo-economic modeling of an indirectly coupled solid oxide fuel cell/gas turbine hybrid power plant," Journal of Power Sources, Vol. 195, No. 24, Dec. 15, 2010, pp. 8134-8140.

8. Halimi, D., Hafaifa, A., and Boua, E., "Maintenance actions planning in industrial centrifugal compressor based on failure analysis," Journal of Maintenance and Reliability, Vol. 16, No. 1, January-March 2014, pp. 17-21.

9. Halimi, D., Hafaifa, A., Bouali, E., and Guemana, M., "Use modeling as part of a compressor maintenance program," Gas Processing, September-October 2014, pp. 55-59.

10. Richecoeur, F., Schuller, T., Lamraoui, A., and Ducruix, S., "Analytical and experimental investigations of gas turbine model combustor acoustics operated at atmospheric pressure," Comptes Rendus Mécanique, Vol. 341, No. 1-2, January 2013, pp. 141-151.

11. Halimi, D., Hafaifa, A., and Bouali, E., "Maintenance actions planning in industrial centrifugal compressor based on failure analysis," Eksploatacja i Niezawodnosc - Maintenance and Reliability, Vol. 16, No. 1, January 2014, pp. 17-21.

12. Wu, X.J., Huang, Q., Zhu, X.J., "Thermal modeling of a solid oxide fuel cell and micro gas turbine hybrid power system based on modified LS-SVM," International Journal of Hydrogen Energy, Vol. 36, No. 1, January 2011, pp. 885-892.

13. Gertler, J.J. and Singer, G., "A new structural framework for parity equation-based failure detection and isolation," Automatica Journal, Vol. 26, No. 2, February 1990, pp. 381-388.

14. Noiray, N. and Schuermans, B., "Deterministic quantities characterizing noise driven Hopf bifurcations in gas turbine combustors," International Journal of Non-Linear Mechanics, Vol. 50, April 2013, pp. 152-163.

15. Nikpey, H., Assadi, M., Breuhaus, P., and Mørkved P.T., "Experimental evaluation and ANN modeling of a recuperative micro gas turbine burning mixtures of natural gas and biogas," Applied Energy, Vol. 117, Mar. 15, 2014, pp. 30-41.

16. Er, O., Yumusak, N., and Temurtas, F., "Chest diseases diagnosis using artificial neural networks," Expert Systems with Applications, Vol. 37, No. 12, December 2010, pp. 7648-7655.

17. Wahba, E.M. and Nawar, H., "Multiphase flow modeling and optimization for online wash systems of gas turbines," Applied Mathematical Modelling, Vol. 37, No. 14-15, August 2013, pp. 7549-7560.

18. Willsky A.S., "A survey of design methods for failure detection in dynamic systems," Automatica Journal Vol. 12, No. 6, November-December 1976, pp. 601-611.

Benrabeh Djaidir ([email protected]) is a Ph.D student in automation systems at the University of Djelfa, Algeria, and a member of its applied automation and diagnostics industrial laboratory. He holds an MS (2012) in industrial instrumentation maintenance from University of Djelfa. Djaidir's work focuses on failure-mode analysis.