Probabilistic approach evaluates reliability of pipelines with corrosion defects

Probabilistic study

A limit state function (LSF) defining the failure mode studied can assess a pipeline's residual life. Equation 1 expresses this function according to the theory of reliability and for a given corrosion defect. LSF is positive (Pf > Pop) for the safe region and negative for the failure region (Pf ≤ Pop) and depends on the same parameters as the failure pressure Pf , the operating pressure Pop, and the corrosion defect dimensions (Equation 2).¹²

Any prediction of the state of the pipeline is based on the prediction of the size of the corrosion defects detected during the inspection. If the depth and length variation rates of a corrosion defect are known, then the dimensions of the depth and length of the defect at time T are defined by Equations 3 and 4. This article treats corrosion rates Vd and VL as constants determined by Equation 5.8 12-15 With ΔTe ≥ 15 years, Equation 6 calculates the probability of a corrosion defect failure.

Monte Carlo method

The Monte Carlo (MC) simulation method calculates the probability of failure represented by Equation 6 by introducing the variables of the LSF as random variables (Equation 7). To account for correlation between the input variables, the correlation coefficient ρXY (-1 ≤ ρXY ≤ -1) is defined by Equation 8.

The larger the absolute value of correlation coefficient ρXY is, the stronger the dependence of Variable X on Variable Y will be. Implementing the Monte Carlo method with correlated variables uses the Nataf transformation consisting of the following steps:^{9 16 17}

• Generating random variables Yi (Y1, Y2...) that follow the standard normal distribution N(0,1).

• Calculating the correlation matrix ρ' of the input variable using Equation 9.^{16 17}

• Transforming the independent variables Yi (following N(0,1)) to correlated variables following standard normal distribution by the orthogonal transformation (Equation 10).

• Converting the variable Zi (Z1, Z2, ...) to the desired correlated variables Xi (X1, X2, ...) by the inverse transformation (Equation 11). Otherwise, two correlated variables X1, X2, which follow the normal distribution N (μ, σ2) will be expressed by Equations 12 and 13. If the correlated variables follow the lognormal distribution LogN(μ, σ2), Equations 14 and 15 apply.

Case study

An X52-grade, 26-in. OD crude pipeline under constant pressure served as the test bed to study the effect of the correlation between the variables of the limit state function and the number of corrosion defects on the reliability of a corroded pipeline by using several failure pressure standards (OGJ, Jan. 5, 2015, pp. 80-85). Table 2 shows the input parameters (LSF variables) encompassing correlated and uncorrelated variables for single and multiple corrosion defects.

Failure probabilities

This article assumes that corrosion defect dimensions (L0 and d0) are correlated, since they are controlled by the same defect. Fig. 1a shows a variation in the pipeline failure probability based on the correlation coefficient (where ρ = 0 represents the case of the independent variables and ρ = 0.3, 0.6, and 0.9 were chosen as dependent variable) for different standards. An increase in the correlation coefficient corresponds to an increase in the failure probability.

Figs. 1b and 1c represent the variation in PF calculated by the Monte Carlo method, with uncorrelated variables (where ρ = 0) corresponding to Fig. 1b and correlated variables (ρ = 0.6) shown in Fig. 1c in terms of time, T, and for different failure pressure standards. Failure probabilities PF in the case of ρ = 0.6 are always higher than those when ρ = 0. The failure probabilities given by FITNET FFS and Shell-92 are higher than those given by other standards, and the B31G standard provides the most nonconservative results. The Netto-Teixeira standard becomes more non-conservative after T = 4 years of service.

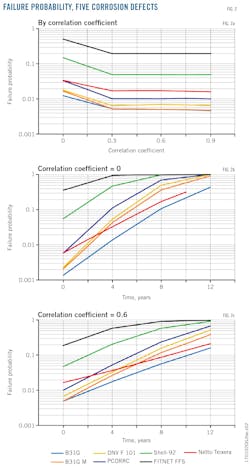
When dealing with a number of corrosion defects (n = 5 in this example) their depths, d0i, (d01, d02, d03, d04. and d05) are both uncorrelated and correlated (Equation 16). Fig. 2a shows that the failure probabilities with correlated variables (ρ = 0.3, 0.6 and 0.9) are smaller than those with independent variables (ρ = 0). This means that the independent variables' case gives more conservative results.

In the range of correlation coefficients between 0 and 0.3, the decrease in failure probabilities is important and between 0.3 and 0.9 it is unimportant. Fig. 2b and 2c represent the two cases (uncorrelated ρ = 0 and correlated ρ = 0.6 variables) in terms of time, T, again for different failure pressure standards. Results were similar to those found when dealing with a single defect. In the case of several corrosion defects, B31G standard was the most nonconservative, followed by the Netto-Teixeira standard after T = 4 years for ρ = 0 and T = 6 years for ρ = 0.6. FITNET FFS and Shell-92 standards gave higher failure probabilities, as confirmed in previous work.

For a single corrosion defect when L0 and d0 are correlated, the larger the correlation coefficient the more conservative the results obtained, compared with the case where L0 and d0 are independent, which gives nonconservative results. In the case of five corrosion defects non-correlation gives conservative results compared with correlation.

The failure probability over time is more important for the Fitnet FFS and Shell-92 standards, making them more conservative than B31G and Netto-Teixeira after roughly 4 years. The modified B31G, DNV F101, and PCORRC standards give average values.

References

1. ASME-B31G, "Manual for determining the remaining strength of corroded pipelines: A supplement of ASMEB31G Code for pressure piping," New York, ASME, 1991.

2. ASME-B31G, "Manual for determining the remaining strength of corroded pipelines: A supplement of ASME B31G code for pressure piping," New York, ASME, 1995.

3. Teixeira, A.P., Soaresa, C.G., Netto, T.A., and Estefen, S.F., "Reliability of pipelines with corrosion defects," International Journal of Pressure Vessels and Piping, Vol. 85, No. 4, April 2008, pp. 228-237.

4. "Corroded pipelines, recommended practice," RP-F101, Det Norske Veritas, Elendom AS, 1999.

5. Leis, N., Stephens, D.R., "An alternative approach to assess the integrity of corroded line pipe, Prat I current status and II alternative criterion," International Offshore and Polar Engineering Conference, Honolulu, May 25-30, 1997.

6. Klever, F.J. and Stewart, G., "New developments in burst strength predictions for locally corroded pipes," International Conference on Offshore Mechanics and Arctic Engineering, Copenhagen, June 18-22, 1995.

7. Kocak, M., Webster, S., Janosch, J.J., Ainsworth, R.A., and Koers, R., "FITNET fitness-for-service procedure," Vol. 1, GKSS Research Center, 2008

8. Qian, G., Niffenegger, M., and Li, S., "Probabilistic analysis of pipelines with corrosion defects by using FITNET FFS procedure," Corrosion Science, Vol. 53, No. 3, March 2011, pp. 855-861.

9. Qian, G., Markus, N., Zhou, W., and Shuxin, L., "Effect of correlated input parameters on the failure probability of pipelines with corrosion defects by using FITNET FFS procedure," International Journal of Pressure Vessels and Piping, Vol. 105-106, May-June 2013, pp. 19-27.

10. Qian, G., Niffenegger, M., Karanki, D.R., and Li, S., "Probabilistic leak-before-break analysis with correlated input parameters," Nuclear Engineering Design, Vol. 254, January 2013, pp. 266-271.

11. Leon, D.D. and Macias, O.F., "Effect of spatial correlation on the failure probability of pipelines under corrosion," International Journal of Pressure Vessels and Piping, Vol. 82, No. 10, October 2005, pp. 123-131.

12. Caleyo, F., Gonzalez, J.L., and Hallen, J.M., "A study on the reliability assessment methodology for pipelines with active corrosion defects," International Journal of Pressure Vessels and Piping, Vol. 79, No. 1, January 2002, pp. 77-86.

13. Sheickh, A.K. and Hansen, D.A., "Statistical modeling of pitting corrosion and pipeline reliability," Corrosion, Vol. 46, No. 3, March 1990, pp.190-196.

14. Ahammed, M. and Melchers, R.E., "Reliability estimation of pressurized pipelines subject to localized corrosion defects," International Journal of Pressure Vessels and Piping, Vol. 69, No. 3, December 1996, pp. 267-272.

15. Ahammed, M., "Probabilistic estimation of remaining life of a pipeline in the presence of active corrosion defects," International Journal of Pressure Vessels and Piping, Vol. 75, No. 4, April 1998, pp. 321- 330.

16. Der Kiureghian, A. and Liu, P., "Structural reliability under incomplete probability information," Journal of Engineering Mechanics, Vol. 112, No. 1, January 1986, pp. 85-104.

17. Chang, C., Tung, Y., and Yang, J., "Monte Carlo simulation for correlated variables with marginal distribution," Journal of Hydraulic Engineering, Vol. 120, No. 3, March 1994, pp. 313-344.

The authors
Mohamed el Amine Ben Seghier ([email protected]) is a PhD student at University of Boumerdes, Algeria. He holds a masters degree (2015) in transportation and distribution of hydrocarbons. He is a member at the University of Boumerdè;s' Laboratory of Reliability of Hydrocarbon Equipment and Materials. His research interests include pipeline integrity, reliability and rehabilitation, and corrosion.
Mourad Bettayeb ([email protected]) is a researcher and assistant professor at the University of Boumerdè;s' Laboratory of Reliability of Hydrocarbon Equipment and Materials. He holds a graduate degree in aeronautic engineering from the University of Blida, Algeria. After working for a short time in that industry, he entered the University of Liege, Belgium, where he received a European diploma in applied science, advanced solid mechanics, and structures calculation. Bettayeb's research interests include, oil and gas equipment reliability, pipeline reliability and rehabilitation, and materials.
Elahmoune Bouali ([email protected]) is a researcher and director at the University of Boumerdè;s' Laboratory of Reliability of Hydrocarbon Equipment and Materials. He holds a graduate degree in hydrocarbon engineering from the University of Boumerdè;s and a PhD in safety of integrity engineering systems (1987) from the University of Oil and Gas in Moscow, Russia. His research interests include reliability systems and optimization, maintenance, intelligent systems, oil and gas equipment reliability, pipeline reliability, and vibration detection and isolation.
Mohamed Gaceb ([email protected]) leads a research team on materials behavior and technology at the University of Boumerdè;s. He graduated in mechanical engineering (1980) from the University of Sheffield, UK, and received his PhD (1985) in the same field from Sheffield Hallam University. From 1986-89 he worked as head of the fracture mechanics subdivision at the Research Centre for Energy Conversion Systems in Algiers, moving from there to become a senior lecturer at the University of Blida until 1998. His research interests include component integrity, materials behavior and technology, fracture mechanics, coatings, welding and non-destructive testing, maintenance, oil and gas equipment reliability, and pipeline reliability.