Fuzzy logic addresses turbine vibration on Algerian gas line
Abdelhafid Benyounes
Ahmed Hafaifa
University of Djelfa
Algeria
Guemana Mouloud
University of Medea
Algeria
Traditional techniques for addressing vibration in gas turbines are unable to adapt to complex modern operating environments. Uncontrolled dynamic vibration can lead to premature aging of turbine components, or unacceptable noise and vibration. To achieve operational efficiency in gas turbine control, this article proposes new methods based on artificial intelligence tools and applies them to Sonatrach’s gas compression station Medjebara SC3 in Djelfa, Algeria, on the Hassi R’mel-Bejaia (GG1) pipeline, part of a 1,400-km natural gas line connecting Algeria to Europe. This article proposes using fuzzy-logic techniques to examine a gas turbine system that includes several interacting components, the failure of which could lead to both lost revenues and lost lives.
This study will first examine the contribution of fuzzy techniques to the modeling of different control parameters of the gas turbine, allowing development of a comprehensive model based on fuzzy clustering, using algorithms based on fuzzy inference systems for classification of real data from the examined turbine. It will then examine and illustrate the obtained fuzzy model’s usability on the SC3 turbine. Results show the effectiveness of the proposed approach.
Fuzzy modeling
Implementing the laws governing equations of complex operating systems typically requires a model too complex to implement. This study required the use of modeling techniques developed from measuring system input and output.
Fuzzy identification and modeling from experimental data are effective tools for approximating industrial systems. Takagi-Sugeno (TS) is among the widely used models. Classification combines with least-square techniques to build the TS model. In this article, fuzzy clustering and the different algorithms associated with it will be used to model the gas turbine based on real data.
Fuzzy clustering algorithm
The fuzzy clustering algorithm is a benchmark among the different methods of fuzzy clustering based on minimization of the objective function given by Equation 1, and determination of the required vector by Equation 2. Equation 3 presents the standard quadratic distance for the space in question, defining the distance between observation and Zk (center) within the metric induced by A and m∊[0,∞] and indicating the fuzzy degree of the partition.
In Equation 2, the measurement of non-similarity expressed by the term JFCM(Z, U, V) is the sum of the squared distances between each vector and the combined Vi and Zk-center of the corresponding class. The degree of activation,Equations 3 and 4 minimize the objective function of Equation 1.
To apply the algorithm to data set Z we chose the class number, 1≺c≺N, the exponent m ≺ 1, with stopping tolerance ε, and the standard matrix, A; randomly initializing partition matrix U after repeating the operation for l=0,1,2.
Equation 5 calculated the cluster centers, and Equation 6 the cluster centers’ distances.
Equation 7 updates the partition matrix if Dika0≻0 for 1 ≤ i ≤ c,1 ≤ k ≤ N allowing operation of the proposed algorithm (Equation 8).
The matrix chosen, A, determines form class in the equation of the objective function. The particular choice, A=I, induces the standard Euclidean norm given by flowing Equation 9.
When expert knowledge is not available, data must identify the structure in question. A fuzzy classification method can then partition the data into classes. Each of these classes, or fuzzy regions, is characterized by a vector called class center. An audit determining degree of similarity groups the data. An appropriate distance measure, quantifying both the distance between data represented as points in the feature space and groups of centers, feeds this audit.
Fuzzy-logic controller
Fuzzy controllers are mainly used in system control for industries. The fuzzy-logic controller includes the following main functions:
• Fuzzification.
• Inference engine.
• Rule-based design.
• Defuzzification.
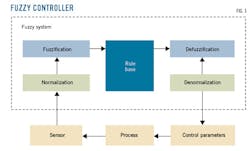
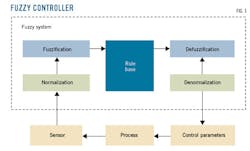
Fig. 1 shows a fuzzy controller block diagram. Fuzzification is the process of converting real scalar value into fuzzy classes. This article uses the Gaussian membership function for inputs and a triangular membership function for outputs. The inference engine decides how to process rules using fuzzy input.
Inputs for the fuzzy controller are error and change in error. The control signals vary according to these parameters. Once the fuzzy controller receives input, the rule base is evaluated. The rule base is built using if-then statements with two input conditions and one output response. Defuzzification is the process of converting the degrees-of-membership output linguistic variables into concrete values.
Process description
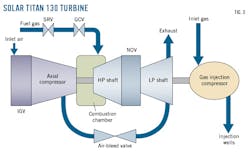
The SC3 gas compression station is equipped with a Solar Titan 130 gas turbine (Fig. 2) and auxiliary equipment. The Solar Titan 130 gas turbine consists of three main sections: the axial compressor, the combustion chamber, and the turbine. There is also a variable inlet guide vane (IGV) in the axial compressor’s inlet and a variable nozzle guide vane (NGV) in its turbine section.
Two valves at the inlet fuel line of the combustion chamber are the main controlling devices of the gas turbine: one controlling inlet fuel pressure, the stop ratio valve (SRV), and one governing load-shaft speed, the gas control valve (GCV).
Application results
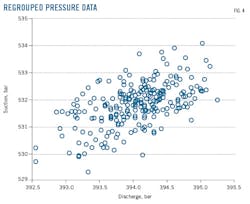
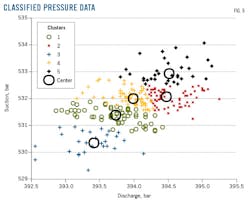
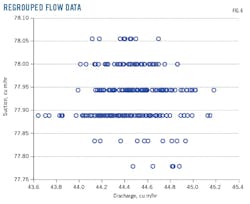
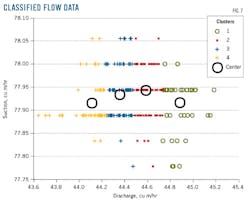
Fuzzy clustering provided initial training of a Takagi-Sugeno inference system by extracting a set of rules that model gas turbine data behavior, using separate sets of input and output data as arguments in creating a training algorithm. Fig. 4 and 5 show the data clusters and their centers. Fig. 6 and 7 show these data regrouped and classified.
An algorithm called fuzzy c-means collects the data into the fuzzy subsets or “clusters” based on similarities. Modelling should not be done across the entire range of operations data-e.g., startup, shutdown, normal operation-but should instead use a different model for each mode. This article further divided the turbine into its subsections, including axial compressor, high-pressure (HP) shaft, low-pressure (LP) shaft, fuel system, and exhaust system.
Equations 10 and 11 model the axial compressor’s two main variables: discharge temperature (ACDT) and pressure (ACDP). Equation 12 expresses normal HP shaft operations and Equation 13 normal operations for the LP shaft. Equation 14 models normal exhaust system operations. In all cases Fn,n=1,2...,5 are the fuzzy inference systems trained using real turbine data.
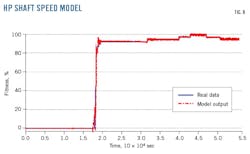
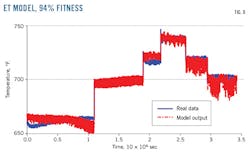
Several hours of turbine data tested and validated this nonlinear model’s accuracy. Fig. 8 shows HP shaft-speed model fitness of 96.14% and Fig. 9 exhaust system fuzzy model validation of 94%. Equation 15 determined level of validation.
A fuzzy clustering algorithm has the essential advantage of automatically generating membership functions, or fuzzy regions, from the data, using a minimizing cost function. This technique plays an important role in achieving optimal data classification.
Fig. 10 shows performance of the fuzzy controller.
Bibliography
Abonyi, J., Roubos, J.A., Oosterom, M., and Szeifert, F., “Compact TS-fuzzy models through clustering and OLS plus FIS model reduction,” IEEE International Conference on Fuzzy Systems, Melbourne, Dec. 2-5, 2001.
Abonyi, J., Babuška, R., and Szeifert, F., “Modified Gath-Geva fuzzy clustering for identification of Takagi-Sugeno fuzzy models,” IEEE Transactions on Systems Man and Cybernetics, Part B: Cybernetics, Vol. 32, No. 5, October 2002, pp. 612-621.
Babuška, R. and Verbruggen, H.B., “Identification of composite linear models via fuzzy clustering,” European Control Conference, Rome, Sept. 5-8, 1995.
Babuška, R., “Fuzzy Modeling for Control,” Vol. 12 de International Series in Intelligent Technologies, Kluwer Academic Publishers, Norwell, Mass., 1998.
Bakalis, D.P. and Stamatis, A.G., “Incorporating available micro gas turbines and fuel cell: Matching considerations and performance evaluation,” Applied Energy, Vol. 103, March 2013, pp. 607-617.
Beliakov, G., and King, M. “Density based fuzzy c-means clustering of non-convex patterns,” European Journal of Operational Research, Vol. 173, No. 3, Sept. 16, 2006, pp. 717-728.
Bezdek, J.C., “Pattern Recognition with Fuzzy Objective Function Algorithms,” Kluwer Academic Publishers, Norwell, Mass., 1981.
Bezdek, J.C. and Dunn, J.C., “Optimal Fuzzy Partitions: A Heuristic for Estimating the Parameters in a Mixture of Normal Distributions,” IEEE Transactions on Computers, Vol. C-24, No. 8, August 1975, pp. 835-838.
Buckley, J.J., “Universal fuzzy controllers,” Automatica, Vol. 28, No. 6, November 1992, pp. 1245-1248.
Dunn, J.C., “A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. Journal of Cybernetics and Systems,” Vol. 3, No. 3, January 1973, pp. 32-57.
Gustafson D.E. and Kessel W.C., “Fuzzy clustering with a fuzzy covariance matrix,” IEEE Conference on Decision and Control including the 17th Symposium on Adaptive Processes, San Diego, Jan. 10-12, 1979.
Hafaifa, A., Guemana, M., and Belhadef, R., “Fuzzy Modeling and Control of Centrifugal Compressor Used in Gas Pipelines Systems,” Multiphysics Modelling and Simulation for Systems Design and Monitoring, Applied Condition Monitoring, Vol. 2, Springer International, Cham, Switzerland, pp. 379-389.
Hafaifa, A., Belhadef, R., and Guemana, M., “Modelling of surge phenomena in a centrifugal compressor: experimental analysis for control,” Systems Science & Control Engineering: An Open Access Journal, Taylor & Francis, Vol. 2, No.1, Aug. 22, 2014, pp. 632-641.
Hafaifa, A., Mouloud, G., and Attia D., “Vibration supervision in gas turbine based on parity space approach to increasing efficiency,” Journal of Vibration and Control, Vol. 21, No. 8, June 2015, pp. 1622-1632.
Hafaifa, A., Mouloud, G., and Attia D., “Fault detection and isolation in industrial systems based on spectral analysis diagnosis,” Intelligent Control and Automation Journal, Vol. 4, No. 1, February 2013, pp. 36-41.
Hafaifa, A., Ahmed, Z.D., and Attia, D., “Fault detection and isolation in industrial control valve based on artificial neural networks diagnosis,” Journal of Control Engineering and Applied Informatics, Vol. 15, No. 3, March 2013, pp. 61-69.
Hafaifa, A., Attia, D., and Mouloud G., “SCADA for Surge Control: Using a SCADA Network to Handle Surge Control in Gas Suppression Systems in Pipelines,” Control Global Journal ISA Transactions, Vol. 24, No. 3, March 2011, pp. 69-71.
Hafaifa, A., Ferhat, L., and Kouider, L., “Fuzzy logic approach applied to the surge detection and isolation in centrifugal compressor,” Automatic Control and Computer Sciences, Vol. 44, No. 1, January 2010, pp. 53-59.
Halimi, D., Hafaifa, A., and Bouali, E., “Maintenance actions planning in industrial centrifugal compressor based on failure analysis,” Maintenance and Reliability, Vol. 16, No. 1, January 2014, pp. 17-21.
Hao, Y., “General interval type-2 Mamdani fuzzy systems are universal approximators,” Meeting of the North American Fuzzy Information Processing Society, New York, NY, May 19-22, 2008.
He, F., Li, Z., Liu, P., Ma, L.W., and Pistikopoulos, E.N., “Operation window and part-load performance study of a syngas fired gas turbine,” Applied Energy, Vol. 89, No. 1, January 2012, pp. 133-141.
Lamfon, N.J., Najjar, Y.S.H., and Akyurt, M., “Modeling and simulation of combined gas turbine engine and heat pipe system for waste heat recovery and utilization,” Energy Conversion and Management, Vol. 39, No. 1-2, January 1998, pp. 81-86.
Launder, B.E., “Modelling of turbulent flow in gas-turbine blading: achievements and prospects,” International Journal of Heat and Fluid Flow, Vol. 3, No. 4, December 1982, pp. 171-184.
Lee, H. and Tomizuka, M., “Robust adaptive control using a universal approximator for SISO nonlinear systems.” IEEE Transactions on Fuzzy Systems, Vol. 8, No. 1, January 2000, pp. 95-106.
Lim, S.C., Park, S.M., and Kim, K.I., Vibration control of high-speed rotor systems using electrorheological fluid, Journal of Sound and Vibration, Vol. 284, No. 3-5, June 2005, pp. 685-703.
Mouloud, G., Hafaifa, A., and Aissani, S., “New approach of calibration in orifice flow meters applied in industrials gas pipeline systems to savings on maintenance costs,” Hydrocarbon Processing, August 2011, Vol. 90, No. 8, pp. 63-68.
Pedrycz, W. and Rai, P., “Collaborative clustering with the use of Fuzzy C-Means and its quantification,” Fuzzy Sets and Systems, Vol. 159, No. 18, Sept. 16, 2008, pp. 2399-2427.
Ruspini, E.H., “A new approach to clustering,” Information and Control, Vol. 15, No. 1, July 1969, pp. 22-32.
Takagi, T. and Sugeno, M., “Fuzzy identification of systems and its applications to modelling and control,” IEEE Transactions on Systems Man and Cybernetics, Vol. SMC-15, No. 1, January-February 1985, pp. 116-132.
Wang, D.G., Han, B.C, and Huang, M., “Application of Fuzzy C-Means Clustering Algorithm Based on Particle Swarm Optimization in Computer Forensics,” Physics Procedia, Vol. 24, Part B, 2012, pp. 1186-1191.
Yang, J., Liu, D.R., Feng, J., and Zhang, H.G., “Controller Design for a Class of Nonlinear Systems Based on Fuzzy Hyperbolic Model,” World Congress on Intelligent Control and Automation, Dalian, China, June 21-23, 2006.
The authors
Abdelhafid Benyounes is a PhD candidate in the applied automation and industrial diagnostics laboratory at Djelfa University, Algeria. He earned an MS (2011) in industrial control engineering from University of M’Sila, Algeria. Research interests include fault-tolerant control using fuzzy logic with decision support in the supervisory system.
Ahmed Hafaifa ([email protected]) is associate professor in industrial process, automation-diagnosis, and reliability engineering in the science and technology faculty of the University of Djelfa. He is also director of the university’s applied automation and industrial diagnostics laboratory.
Guemana Mouloud is associate professor at the University of Boumerdes, Algeria. He earned both his PhD (2012) in industrial maintenance and his MS (1998) in mechanical engineering at the University of Boumerdes. Research interests include industrial maintenance, system reliability, dynamic systems, and diagnostic optimization.