Assessing economic worth in hydrocarbon exploration
Professor Lerche examines how a company can option an investment opportunity with a minimum rate of return requirement and shows how to address quantitatively the various constraints and their influence on project economics.
Ian Lerche, University of Leipzig, Leipzig, Germany
One of the more difficult problems to assess for economic worth in hydrocarbon exploration occurs when a corporation has a requirement that must be satisfied before the corporation will consider investing in a potential opportunity. In particular, consider the most usual situation where the estimate of potential gains (G), costs (C), and probability (p) of achieving the gains are such that the estimated mean rate of return (pG/C) is smaller than the minimum value the corporation will allow in order to invest.
The corporation then has two options: either it chooses not to invest in the opportunity or it chooses to take out an option to invest later in the opportunity. The option to invest is considered in conjunction with undertaking further investigations that are to provide new information which, it is hoped, will change the assessments of possible gains, and the probability of achieving the gains, in a positive manner so that the potential opportunity then has a higher rate of return – larger than that required by the corporation. The new information may, however, show a lower potential gain than previously estimated or a lower chance of achieving a gain, so that the result would be that the corporation then still chooses not to invest.
There is an associated cost of the option to invest, which is lost if the corporation chooses not to be involved after the new information is available. There is also a cost associated with obtaining the new information that has to be borne by the corporation irrespective of whether or not the corporation chooses to participate in the opportunity after assessing the changes the new information brings to the potential opportunity. These extra costs increase the total costs and so, in order to obtain a rate of return higher than the corporate required minimum, the gains and/ probability of achieving them assessed on the basis of the newly acquired information must also be increased to cover these additional costs and still keep the estimated rate of return higher than the corporate minimum demanded.
There are several questions one can ask of this economic system. For a given option payment, what is the maximum cost one should invest to obtain new information? Alternatively, one can ask: How much should one pay for the option to choose to invest in the opportunity at a later time and how is the cost of obtaining new information limited by the corporate minimum rate of return requirement and by the amount one has paid out for the option to invest later? Or again, how great an increase must the new information bring to the prior estimations in order that the corporate minimum rate of return requirement is achieved or exceeded?
The purpose of this article is to provide quantitative answers to such questions. In addition, when it is remembered that the assessments are just that - assessments made prior to undertaking any drilling - then there must be an uncertainty associated with any and, indeed, all parameters. An associated question is then: How do the uncertainties in the parameters influence the chances that the new information will determine that the corporation should, or should not, invest in the opportunity?
Mathematical analysis
Let the estimated costs of the opportunity be C, the potential gains estimate be G, and the probability of achieving these gains be p. The expected value of the opportunity is then E = pG-C, with a standard error, s, around the expected value given through s2 = p(1-p)G2.
The corporation demands a minimum expected rate of return, MROR on any opportunity before it will permit investment. Now the expected ROR for a project is given by pG/C so that if pG/C< MROR then the corporation will not invest. Suppose the original opportunity figures are such that they do not satisfy the corporate criteria for investment. However, suppose also that the information used to assess the potential gains and the probability of achieving those gains s limited, as s the usual situation in an exploration project. The corporation does not wish to condemn the project out of hand based on sparse data used to make the estimates. Accordingly, the corporation takes out an option, at a cost $, to permit it to invest in the opportunity at a later date if the corporation so chooses, after the corporation undertakes to obtain further information, at a cost to the corporation of Cn.
Let the new information change the estimated gains to be made from the opportunity to g, and let the probability of obtaining such gains also be changed to P. The corporation will then choose to invest in the opportunity if Pg/($+C+Cn) > MROR, else the corporation will not invest and will write off the total costs of $ +Cn. This situation is sketched in Fig. 1. But even when the corporation does invest there is no guarantee it will realize the gains estimated, there is only a probability P that such gains will happen with a probability 1-P that there will be no gains and so a loss of C+Cn+$, as depicted in figure 1. To quantify the depiction of Fig. 1, introduce the function S(x) that takes on the value 1 if x>0, and the value -1 if x<0.
Then one can write the expected mean value, E(after), after optioning and acquiring new information as (Equation 1):
- E(after) = [1 + S(Pg - C - Cn - $)][Pg - C - Cn - $]/2 +[1 - S(Pg - C - Cn - $](- C - Cn- $)/2.
One can write the standard deviation, s(after) around the expected mean value through (Equation 2):
- s(after)2 = [1 + S(Pg - C - Cn - $)]P(1 - P)g2/2
The corresponding Gaussian cumulative probability that one will obtain a worth of W or greater from the opportunity is then given through (Equation 3):
where (Equation 4):
- A = [W-E(after)]/[21/2s(after)]
In addition to the corporate requirement that the expected ROR exceed a corporate minimum, usually a corporation is also concerned about the chances of realizing a profit. Accordingly, a corporation often sets a second requirement in place: The cumulative probability of obtaining a worth W in excess of a lower corporate minimum worth of X must exceed MAC, the corporate Minimum Acceptable Chance, or the corporation will not invest in the project despite the amount it has already spent on the option costs and the new information costs. Thus the corporation also requires (Equation 5):
- P(X) >MAC
where P(X) is just Equation 3 evaluated at W = X.
It is the combined effect of all three of the constraints that is of interest in determining what it is a corporation should do. One has to juggle the corporate mandates on minimum ROR, MAC, and minimum expected worth X in terms of the amounts the corporation should spend on the option and on new information.
It can also be that the corporation sets the requirements too high so that there is no way, even with low costs for the option and also for new information, that one can satisfy all three requirements. In such a case the corporation should have abandoned the opportunity prior to spending money on the option and also on the new information.
When the constraints are satisfied, then there is still a maximum worth, Wmax, that will just satisfy the requirement that P(Wmax) > MAC because the cumulative probability of obtaining a worth in excess of W decreases as W increases. Thus there is then a range of cumulative probability values and a range of worth values where both P > MAC can be satisfied and also where Wmax >W > X is valid. If X is set too high then the range shrinks to zero and there is then no way to satisfy the three corporate requirements. Under such conditions the corporation does not invest in the opportunity because its corporate criteria are not met. Instead the corporation walks away from the opportunity at a guaranteed 100 % loss of Cn+$.
Note also the requirement that the anticipated rate of return Pg/(C +Cn +$) > MROR can be written in the form (Equation 6):
- 0 < $ + Cn <(Pg/MROR) – C
which already requires that C < Pg/MROR in order to be satisfied at all, and when C is less than Pg/MROR then Equation 6 sets a limit on the combined option plus new information costs in order to satisfy the first corporate mandate of a required minimum rate of return should the corporation decide to invest in the opportunity. The second and third requirements of a high enough cumulative probability to exceed MAC and of a worth value range greater than X then limit further the allowed option plus new information costs.
To illustrate the influence of all three constraints we have constructed an Excel spreadsheet program based on the above mathematical precepts. This numerical aspect forms the basis for the next part of the article.
Numerical illustrations
As a basic set of parameters prior to optioning and acquiring new information, consider that an opportunity has an assessed cost of C = $20MM, a probability that the venture, if undertaken will find hydrocarbons of p = 0.25 and that the gains to be made from the hydrocarbons are estimated at G = $400MM. In this case the anticipated mean rate of return is pG/C = 5.
Let the corporation have in place a mandated minimum ROR of MROR = 2, so that the corporation is prepared to invest in the opportunity without any change in the assessed values for G and/or p. However, the corporation wishes to retain the option to invest at some future date if the addition of information would make the opportunity appear more palatable.
The corporation is prepared to pay an option price plus acquisition of new information price at a combined maximum of 50% of the costs of the opportunity, i.e. a total of $10MM. Now if the corporation spends all of the $10MM on the option, then there is nothing left over to acquire new information and so the estimates of p and G can hardly be changed. It is also then a waste of money to spend all the $10MM on the option because the corporation spends nothing on acquiring new information and so could have saved the $10MM it laid out for the option.
On the other hand, if the corporation chooses to spend the $10MM on the acquisition of new information, then there is no option payment possible and so the corporation loses the right to invest in the opportunity. In either of these two extreme cases the corporation will not undertake investment: if no new information can be acquired then the opportunity will still have an estimated ROR less than the corporate required minimum, while at no option payment the right to participate at some future date is forfeit. There must then be an intermediate position possible where both the option amount plus the money used to acquire new information are balanced to keep an option alive and also to supply better estimates of the success probability and the potential gains from newly acquired information.
In actual situations, the problem is more complex. The choice of the option amount is rarely dependent on the corporation but either on partners in the opportunity or on leasing agencies who set up the conditions for lease, exploration, development, and production.
As an illustration, take it that the option amount is 10% of the estimated opportunity costs, i.e. a cost of some $2MM, leaving the corporation with about $8MM for acquisition and interpretation of new information prior to deciding whether to participate in the opportunity or not. But the corporation must not necessarily spend the full $8MM on acquisition and interpretation of new data; the more that is spent then the higher must be either or both of the probability of success and/or the gains that one hopes to make.
These needs are to ensure an estimated ROR that exceeds the corporate minimum required, as well as an estimated cumulative probability that exceeds the corporate demanded MAC, and also a potential worth that will exceed the minimum worth the corporation will accept in order to proceed. The more the corporation spends on new information the more difficult it is to ensure the corporate mandates are satisfied.
The ultimate questions that need to be answered are: What are the estimates of the costs, the probability of success, and anticipated gains so that one can quickly determine whether there is a chance of attaining the minimum ROR and the MAC set by the corporation? And, once these demands are met, what then is the option amount that one should pay in order to ensure some degree of profitability, assuming one can indeed make a profit satisfying the corporate requirements?
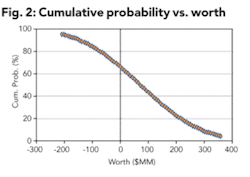
Figure 2 shows the cumulative probability of obtaining a worth for the canonical parameters given above, together with $2MM reserved for the option costs and $6Mm spent additional information (out of a total $10MM the corporation could choose to spend on the combined option costs plus additional information), indicating there is about a 65% chance of obtaining a positive worth.
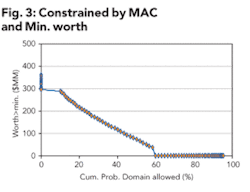
However, when one imposes a minimum worth requirement of $30MM together with a MAC of 10% or greater then Figure 3 shows the worth exceeding the minimum desired as a function of the acceptable cumulative probability range, while Figure 4 shows the reverse curve of cumulative probability as a function of desired worth in excess of the minimum. Note that the constraints now limit the cumulative probability of obtaining a chance in excess of the MAC (=10%) and the minimum acceptable worth (=$30MM) to less than 60% cumulative probability.
If one increases the MAC to 50% then, as shown in Figure 5, the chances of obtaining a worth in excess of about $60MM are zero, so that the limits imposed by the corporation severely curtail the chances the corporation will invest in the opportunity.
Discussion and conclusion
The point about the two simple illustrations is that they show how to go about construction quantitative risk models for options plus costs of additional information when a corporation sets not only a limit on how much can be spent in total on the combined option costs plus acquisition of new information but also when the corporation sets stringent limits on the minimum worth the corporation will accept from the project and, in addition, when the corporation sets stringent limits it will accept on the minimum acceptable chance of success. It is this point that the illustrations have been tailored to address as cleanly and as simply as possible.
In a more general sense, the controls of minimum acceptable chance and minimum estimated acceptable worth that a corporation will normally impose on an exploration project, need to be incorporated directly in the assessment of risk of the project. In addition, the costs of an option plus the costs of additional information acquisition need to be incorporated also. The fraction of a limited budget one spends on optioning and the fraction one spends on acquisition of new information do not have to use up the total available budget, as also shown here.
Thus the aim of showing that all these uncertain factors can be incorporated into an exploration project quantitative risk analysis without having to add the corporate concerns in after the fact has been achieved. Naturally, the ability to handle a portfolio of exploration projects can be treated similarly-at least for a large total budget.
For a budget where one is constrained to take only fractions of the projects, perhaps the techniques introduced in Lerche and McKay (1999) for constrained budgets can be used together with the constraint of corporate MAC, limited cash for optioning plus new acquisition, and a corporate mandate of a minimum acceptable worth.
References
Lerche, I. and McKay, J. A., 1999, Economic Risk in Hydrocarbon Exploration, Academic Press, San Diego.
About the Author
Dr. Ian Lerche [[email protected]] has authored hundreds of papers and more than two dozen books. His main professional interests are hydrocarbon exploration and production risk problems, environmental and economic assessment of geohazards, astrophysics, and applied mathematics. He sits on several editorial boards, has received several international awards, including the Levorsen Award of the AAPG, the John Cedric Griffiths Award of the IAMG, and the DuPont Award for Science. He was Nordic Professor of Petroleum Geology 1991, French Academy of Sciences Visiting Professor 1995, DAAD Professor of Geology at the University of Leipzig 2003-2005, and Mercator Professor of Astrophysics at the Ruhr University (Bochum) 2005-2006. He currently resides in Germany.