Risk's sweet spot: How much should you risk?

Larry Hickey,FRM, Risk Limited, Dallas

Risk has a speed limit — a bright shining line separating "good risk," which leads to a higher long–run growth rate of wealth, and "bad risk," which doesn't. This limit separates the responsible oil explorer from the thrill seeker, the risk neutral investor from the volatility junkie, the brave from the foolhardy.

By simply exceeding the speed limit, you can reduce the expected growth rate of wealth all the way down to zero. Speeding in this context means increasing the size of your risk position relative to your risk capital, where risk capital is the wealth or "bankroll" you seek to maximize. And you don't have to exceed the limit by much. If one unit of risk is optimal, your growth rate will be zero at two units.

"Too much of a good thing" may be counterintuitive, but it is borne out by both the math and experience. An overly concentrated portfolio will go broke in the long run no matter how "good" the underlying investments.

Sinking in a rising tide

"Good" investments are risky projects with a positive expected value that if undertaken repeatedly will produce positive returns in the long run. The challenge is how to capture the long–run value of these good investments when the long run is a luxury only enjoyed by those who survive the short run. How can you best capture the edge in the underlying process without going broke along the way?

Expected value vs. growth rate

It's crucial to understand the difference between maximizing the expected value of the underlying process and growth rate of the bankroll.

Consider a coin flip game that pays a generous 2:1 for heads. Fair odds are 1:1. This process has an expected return of 50%.

That looks like a pretty good investment. So you rule out doing nothing and missing out on an opportunity to triple your money. You could risk it all on every flip but then you run a 50% chance of going broke each time. Or you could risk some fraction of your bankroll on each round. What to do?

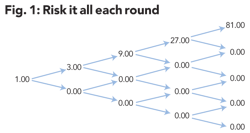
If your objective is to maximize expected value, you should risk it all every time. At the end of four rounds, all value will be concentrated in a single outcome (W–W–W–W) worth 81 times the initial wager. A single lottery ticket hits one out of every 16 times. The other 15 outcomes have no value. The value of the process is 5.0625; a 50% return compounded four times.

But take a look at the range of terminal values. Does it look like a sustainable business or a crapshoot? If this process keeps going, you will go broke. (See Figure 1)

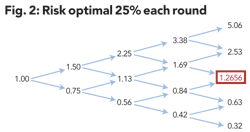
If on the other hand your objective is to maximize the growth rate of your bankroll, the answer is quite different. Risk 25%. So 75% is held in reserve each round. Half the time you will win and your bankroll will be 150%. The 75% in reserve plus 50% won plus your 25% bet. Half the time you will lose and you will be left with just the 75% in reserve. The highest growth rate occurs when the weighted average log of terminal value is highest.

The log function is used to convert a value into a return which can be added across rounds. As shown in Figure 2, the sequence W–L–W–L results in a terminal wealth of 1.265625. That's 2 wins and 2 losses. The log of each win is .4054. The log of each loss is –.2877. Add all 4 together and get .235566. e^.235566 = 1.265625. By the law of large numbers, the cumulative return will converge to the median times the number of rounds.

To make that more concrete, observe the tree diagram below. Ethier (2004) showed that the highest growth rate occurs when the value in the red box, the median outcome, is highest. Look at the range of terminal values. Here we have a sustainable business. (See Figure 2.)

Risking 25% will result in an expected growth rate of 5.889%, higher than the 5.880% for either 24% or 26%. Note that if you risk double the optimal fraction — 50% –– the expected growth rate goes to zero.

Although the "Risk It All" expected value of 5.0625 dwarfs the "Risk Optimal 25%" strategy expected value of 1.60 – a 50% compound return versus a mere 12.5%, the optimal strategy results in a geometrically growing sequence that won't blow up. The "Risk It All" strategy blows up upon the first loss. Clearly, the relevant objective is not to maximize expected value. It is to maximize the growth rate of the bankroll.

The Kelly Criterion

In 1956, John Kelly, working for AT&T's Bell Laboratory, published his method in a paper addressing long distance telephone noise issues. The central problem of decision making under uncertainty had much wider implications. The gambling community soon got wind of the formula implementing it first as an optimal betting system in horse racing and later in blackjack. The formula enabled gamblers to maximize the size of their bankroll over the long term while eliminating the risk of ruin along the way. The system has gone on to be used in capital and commodity markets and has direct applicability to the offshore prospector weighing up the potential risk and returns of oil exploration.

The Kelly Criterion is a function of two variables: the probability of winning (PWIN) and the payout (PAYOUT). Note that PLOSE = 1 — PWIN. The fraction of your bankroll that should be risked on each round is (PAYOUT*PWIN — PLOSE)/PAYOUT. For an even money proposition, where the payout is 1:1, the formula simplifies to 2*PWIN — 1. Note that a payout of 1 means that you receive 2 upon winning; 1 unit won and the 1 unit risked. In simple English, the formula says "risk your edge divided by the payout."

Let's say you have a 52% chance of success and a payout of 1. You should place 4% of your bankroll at risk. On average, if you repeat this 100 times, you will win 52 times and lose 48 times, for a net gain of $4. If you expect to win $4 for every $100 risked, your edge is 4%. With a payout of 1, you risked your edge divided by the payout.

Let's say you have a 37% chance of success and a payout of 2. So if you place $1 at risk, you will either gain $2 or lose $1. By the formula, you should place 5.5% of your bankroll at risk. Do it 100 times. On average you will win $2 37 times and lose $1 63 times, gaining $11. 5.5% is your edge of 11% divided by the payout of 2.

Let's say you only have a 32% chance of success in that same situation with a payout of 2. In order to have a positive expectation, you have to succeed at least 1/3rd or 33.333% of the time. As 32% is less than 33.3%, this project is a loser and no money should be put at risk. Money is only put at risk when there is a positive expectation.

One useful thumb rule emerges from the math. Never risk more than your chance of winning. As established above, if you have 37% chance of success and the payout is 2 to 1, you should risk 5.5%. If the payout is 20 to 1, the optimal fraction moves up to 33.85%. If the payout is 200 to 1, it's 36.685%.

No matter how high the payout, if the chance of winning is 37%, the optimal amount at risk will not exceed 37%. So if the project costs more than your chance of winning times your risk capital, it's too big. If you want to move forward, it's time to find other investors to shoulder some of the risk. It's time for a joint venture. If the project's cost exceeds 2x the Kelly fraction times your risk capital, your long–term expected return is zero and a joint venture is the only way to proceed.

The Kelly Criterion assumes that gains and losses from each round are used to establish the new level of risk capital. So a constant Kelly fraction means greater money risked after wins and less following losses. This dynamic resizing is critical to removing the risk of ruin or going bankrupt before being able to capture the edge of the underlying process.

There is a practical limitation to the model. Investments may not be infinitely divisible. Although the fraction risked each round is constant, after a series of losses that fraction may translate into little money. If your project has a fixed cost, say $4 million dollars to drill an offshore well, any number below $4 million means that some sort of risk sharing is optimal. If your bankroll dips below $4 million and risk sharing isn't a practical option, you are effectively broke.

High volatility

The downside of using Kelly is that portfolio volatility is high. You can't lose all your risk capital, but there is a 1/3 chance of halving the bankroll before it is doubled. In fact, the chance of dropping to 1/n of your risk capital is 1/n. So you have a 50% chance of losing half and a 10% chance of losing 90% of your bankroll, and so on. Many don't have the stomach for Kelly, preferring Half Kelly. Half Kelly will yield at least 75% of the Kelly returns with much less volatility.

As we saw earlier, betting beyond Kelly is counterproductive as the longrun growth rate will fall, dropping to zero at two times Kelly. Because both the payout and probability of winning are estimates that may be in error, shooting for Half Kelly would seem a prudent alternative.

Implementing Kelly

Here is how Kelly can be implemented in an oil exploration environment. Take a look at a representative sample of previous wells. Determine the fraction that were successful, PWIN. Take the dry holes and calculate the average loss. Take the winners and calculate the average gain. The ratio of the average gain to the average loss is PAYOUT. Note that we're making the bold and likely erroneous assumption that the future will mirror the past.

In a trading environment where the edge is likely to be small, the formula is approximately equal to the average gain divided by the variance of outcomes.

A fellow in Omaha

Maybe others in the market have arrived at the same conclusion from a different route. Charles Munger, Warren Buffett's partner, cites the patience to wait for a good investment idea, then to bet heavily on that idea when the odds were stacked in their favor as the single most important factor in their success. That sounds an awful lot like the Kelly Criterion.

Using Kelly?

It's hard to prove if assets are being allocated based on Kelly. It's easier to show when they aren't. Do they have any holdings worth less than 1% of total capital in the portfolio?

Harvesting edge

It is not enough to find investments with positive expected value. The road to ruin can be paved with "good" investments. If you want to translate that edge into a growing bankroll, you will also have to properly size your risk positions. The math is incontrovertible. Size matters.

About the author

Larry Hickey is principal advisor at Risk Limited. He has been an ETRM consultant for the past 12 years. He's also been an FX options trader, a US Navy submarine officer, and a concert promoter. Hickey has an MBA from the University of Washington and a BS degree from the US Naval Academy.

More Oil & Gas Financial Journal Current Issue Articles
More Oil & Gas Financial Journal Archives Issue Articles
View Oil and Gas Articles on PennEnergy.com