Portfolio optimization techniques help allocate capital
Portfolio optimization techniques can provide oil and gas companies a means for determining optimum capital allocation to candidate investment projects, under different constraint conditions.
These techniques must be combined with other methods, which ensure that flexibility is maintained to adjust positions under future changing business conditions.
The efficient allocation of capital among assets is critical for any corporation if it wishes to balance short-term considerations vs. the desire to maximize long-term value. This is especially true in today`s volatile price environment in which companies can have a considerable constraint on spending because of pressure to deliver adequate cash flows and earnings to shareholders.
This article describes a practical method for capital allocation using data derived from conventional asset economic analysis techniques.
A number of analysts, including the authors, are working on methods and processes for optimizing portfolios accounting for risk. These methods require not only more-sophisticated portfolio analysis techniques, but also more-rigorous analysis of individual assets. These methods, not discussed in this article, include:
- Valuing assets according to their exposure to market risk
- Understanding the different components of risk in a portfolio
- Optimizing a portfolio to balance risk and shareholder value
Capital allocation
At its simplest level, portfolio selection consists of solving a capital allocation problem of how much to invest in each set of opportunities, such as spending on exploration, developing a new field, and increasing production near term.
Classical finance texts state that, in theory, the corporation should invest in any asset which has a positive net present value (NPV) when discounted at the appropriate discount rate.1 In practice, however, the corporation will have specific constraints on capital investment and targets it wishes to achieve for cash flow and income.
Maximizing the portfolio value is the generally accepted optimization target. If a single constraint exists, then the optimum portfolio for that constraint condition can be determined by ranking assets according to the ratio of an asset`s contribution to the optimization target over an asset`s contribution to the constraint.
For example, to maximize NPV under a single constraint of the corporation`s spending in a given year, one can rank the assets by the ratio of their NPV to their spending in that year. Then, one can consecutively select the assets with the highest ratios until the spending constraint is met.
For such a simple problem, an optimization model is not needed. But if an optimization model is used, it would give an identical result.
Of course in practice, projects that have a particularly high spending in the chosen year, will have a low ratio of NPV to spending, and are liable to be rejected from the portfolio, although they may be intrinsically excellent projects.
This is why a better method for selecting projects is to use a measure of their long-term spending, such as 5-year or lifetime spending. After tax is preferable to before tax spending.
The ranking of projects on NPV divided by the present value of the total investment or net present value ratio (NPVR) will produce a portfolio that maximizes value given a long-term spending constraint, and will identify intrinsically valuable projects. The reality is that often spending, cash flow, earnings, or production constraints will be imposed in a particular year.
The task facing the portfolio designer is to be able to invest in the most profitable opportunities while meeting these constraints.
If this is the case, linear optimization programs can provide a useful tool for satisfying one or more constraints (such as spending, cash flow, and income) while maximizing the value of the portfolio.
Linear optimization
Linear optimization theory is well established, forms the foundation for the discipline of operational science, and has found many applications in economics, financial planning, social sciences, and engineering.2 In the oil industry, it is often used for optimizing process plant design and operational performance.
Linear optimization models assume that there is a linear relationship between the variables and the optimization target and constraint outcomes.
In the case of an oil and gas portfolio, one variable is the percentage equity holding in each asset. A good approximation is that the value to the corporation of the asset and the associated costs, production, and revenue are linearly related to the corporation`s equity holding in the asset.
The major job in linear optimization is establishing the "feasible solution space" which is the multidimensional space that defines the feasible range of each variable given the constraints on the system and the relationship between variables. After this feasible space is found, the model will find the maximum, or minimum, value of the optimization target within the feasible space.
No feasible solution may exist if there are too many constraints or the constraints are too severe. If there is a feasible solution, a linear optimizer will always find the globally optimum solution, given the constraints.
Optimizer program
There are several commercially available programs designed to optimize a portfolio of assets under a given set of constraints. Normally, the program uses a long-term target, such as maximization of value (NPV) as its optimization criteria, although other criteria may be selected. For example these criteria could include maximization of cash flow in a particular year.
Constraints consist of:
- Portfolio constraints, which apply to the portfolio as a whole and are generally over a shorter term than the optimization criteria. These constraints include restrictions on spending or cash flow (for one or several years) and are to some extent discretionary.
- Asset constraints such as the limitations on equity holding and sale of an asset. These are generally immutable functions of the asset.
The program should also allow the modeling of dependency between assets (for example a satellite field can only be developed if the main field is developed) and allow assets to be bought, sold, or deferred.
The program should allow portfolio optimization under a large number of constraints. The example in Fig. 1 used over 300 projects/assets with as many as 1,000 constraints. The vast majority of these constraints were asset constraints.
Each project/asset consists of several years or lifetime of the appropriate operational/financial data required for normal economic analysis, such as spending, production, cash flow, income, etc. Also, an NPV is required for every project/asset.
The optimization tool chooses (allocates capital to) the projects that maximize NPV while meeting the specified short-term constraints, such as spending, cash flow, income, and production for one or several years.
As has been often shown, linear optimization will always provide a better result than human intuition for problems involving more than one constraint.
Optimization guidelines
Optimization can be approached in many different ways. The steps shown in the box and the following description may serve as general guidelines for someone who is a first time user of these techniques.
Optimize at highest level
Great care should be exercised if affiliate/regional optimization is to be performed, because artificial constraints set by the affiliate or region may eliminate projects that would have been selected at the corporate level. Although the portfolio will be optimum from the affiliate or region`s perspective, it may be less than optimal from that of the corporation`s perspective.
To avoid this problem, a central group should be responsible for optimizing the overall portfolio based on the total corporation constraints/goals such as spending, cash flow, income, and production. To do this, every project or group of projects should have sufficient definition, a same set of assumptions (for example risked economic indicators, net working interest cash flows, etc.), and data consistency (for example same discount rate, same effective discount date).
After determining the strategy that optimizes the total portfolio, with consistent constraints/targets, one can then set the strategy for individual affiliates/regions. These groups then may utilize optimization methods for managing their subportfolio interactively within budget cycles. This consists primarily of project substitution, at the affiliate/regional level, with the goal to always meet the agreed-upon targets.
Ranking opportunities
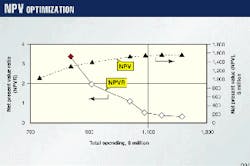
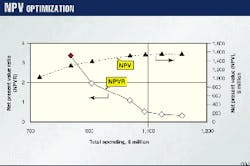
As a first step, it is useful to rank all the opportunities based on NPV divided by the present value of the total investment or NPVR. This can be done either on a spreadsheet or by using the linear optimization tool. A graphical display of the results is also useful (Fig. 1).
In this sample portfolio of about 300 projects, a plot of NPV vs. total spending shows, as expected, that as spending increases, the portfolio`s NPV will increase at a decreasing rate. In other words, the NPVR of the accepted projects decreases with increased spending.
The analyst can then apply the hurdle NPVR to determine the maximum spending for a particular year. Of course, this assumes an ideal world with no cash flow or other constraints.
Robustness of commitments
A portfolio of exploration and production opportunities will include several projects that have commitments, such as drilling obligations and rig commitments. It is a good idea to check the robustness of these commitments vs. noncommitted projects.
In the example (Fig. 1), by not forcing the optimization tool to always fund committed projects, one increased the portfolio`s value by more than 10%. In other words, some committed projects were not as robust as other projects.
Of course, the analyst to determine the final capital allocation needs to apply other knowledge, such as costs to get out of or defer commitments.
Minimize constraints
A general rule for the optimizer is that as more constraints are applied, the greater is the reduction in value.
It is important to remember that the term optimum applies to the portfolio under a given set of constraints. If artificial constraints are applied, the portfolio will not truly be optimized because a greater value could have been obtained if those constraints had not been set.
As an example, if the sample portfolio does not have any constraints in Year 1 compared to constraining cash flow to $10 million (cash flow = net revenues of all projects less the sum of all operating costs, investments and taxes), a higher portfolio value will be obtained for the case without cash flow constraints, as follows:
- Without cash flow constraint: NPV = $1,575 million and Cash flow = -$58 million
- Cash flow constraint in Year 1: NPV = $1,450 million and Cash flow = $10 million.
Of course, having a higher NPV has to be checked compared to the ability of the firm to have a negative cash flow in a given year, particularly in a low-price environment. Also, in practice, spending (which is a key component of cash flow) is used as an optimization variable instead of cash flow.
With the optimization tool, one can set constraints on several variables for one or several years. A useful exercise is to optimize the portfolio to match company goals/targets. For instance if the corporation wishes to maximize value and at the same time meet a Year 1 cash flow of at least $10 million and 86,000 bo/d production, the results would be:
- Without constraints: NPV = $1,575 million, Cash flow = -$58 million, and Production = 85,000 bo/d
- Cash flow and production constraint in Year 1: NPV = $1,395 million, Cash flow = $10 million, and Production = 86,500 bo/d.
By introducing a second constraint, production, one further decreases portfolio value. Again, the maximum value solution, with only a few constraints set and limited asset characteristics represented by the data, may not be feasible. Other information available to the analyst will come into play to decide what is doable from financial and operational points of view.
The analyst also needs to keep an eye on targets beyond the first year. This can be done by setting the appropriate cash flow, production, and income targets for several years, after which the results are optimized and compared with optimization runs without such targets (constraints).
Applying constraints
The application of a single aggregate constraint over a number of years always results in a higher portfolio value than if an equivalent constraint was applied for each year.
For example in the sample portfolio, the objective is to maximize NPV and have a cumulative oil production of 98 million bbl during the next 3 years. In this case, the highest NPV is obtained by allowing the optimization tool to select projects in the 3-year period by setting a 3-year production target of 98 million bbl rather than by setting production targets for each of the next 3 years that add up to 98 million bbl. The results are as follows:
- 3-year single production goal: NPV = $1,557 million
- Yearly production goal for 3 years: NPV = $1,511 million.
The higher NPV for the longer-term case is due to a smoothing effect on the portfolio, especially for a sample of over 300 projects. The tool is better able to select the projects that maximize NPV and reach the production target over a longer time period.
Note that even though the total 3-year production is the same, the yearly production will be different for the two cases.
Asset sales, deferrals
As mentioned before, the linear optimization tool either selects or rejects funding of a project when trying to maximize value. As a subsequent step, one needs to test the portfolio by allowing rejected assets, often mature ones, to be sold and/or deferred into the future when spending/cash flow constraints may be less rigid.
It is important to always reflect the costs of holding assets that are being deferred. These can be substantial.
Another way to test the robustness of the portfolio is to start the optimization process by allowing deferral and/or selling of all assets. The optimization tool will choose the projects that meet the constraints, such as spending. Projects not selected will automatically be sold or delayed.
In summary, linear optimization is one of many tools for assisting in the design of a portfolio. The tool will only determine the optimum solution given a particular set of constraints. The portfolio mixture selected may not be feasible if the set of constraints lacks some elements of the assets` reality.
In addition, it is important to keep in mind that the optimization examples described in this article assumed equal risk for each opportunity and only one set of assumptions for the future. Ideally, the portfolio should include a measure of the risk (standard deviation) of each opportunity and undergo "stress testing" for different future scenarios before accepting any strategic direction it dictates.
It is also critical to have a good and consistent project description because selection of each project is based only on the data supplied, such as NPV, cash flows, and production.
Acknowledgment
All opinions in this article are those of the authors and do not represent Mobil Corp.`s procedures for portfolio optimization.
References
- Brigham, E.F., Financial Management: Theory and Practice , Chapters 11-12, Dryden Press, 1979.
- Taha, H.A., Operations Research: An Introduction, Part 1, MacMillan Co., 1971.
The Authors
Rene Santos was previously a strategic planning advisor for Mobil E&P, Fairfax, Va., and is currently assigned to Mobil Oil in Caracas, Venezuela. Santos holds an MS in petroleum engineering from the University of Texas and an MBA from the University of Houston.
Keir Harman is senior analyst with Indeva Energy Consultants, a U.K. firm specializing in decision management for the oil and gas industry. Harman holds a BS in engineering from the University of Nottingham and an MS in Renewable Energy Systems from the University of Loughborough/Riso National Laboratory, Denmark.