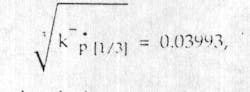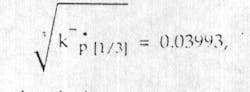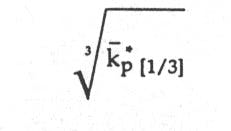Permeability function describes core permeability in stress-sensitive rocks
T.A. JelmertA consistent method for obtaining average permeability functions of stress-sensitive reservoirs is described.
Norwegian University of Science & Technology
TrondheimH. Selseng
Saga Petroleum ASA
Oslo
Traditional core analysis can accommodate pressure-sensitive formations by describing core permeability as a mathematical function rather than a single number.
Results from several cores may be combined into one single curve, provided the permeability functions can be described by two parameters.
The average permeability functions will be useful both for well test and reservoir simulation studies.
Rock properties
Rock properties of stress-sensitive reservoirs are controlled by the effective stress se, which is defined by Equation 1 [158,133 bytes] (see equation box). In Equation 1, so denotes overburden stress, and a is the effective stress-law parameter. Because overburden stress usually remains constant during a well test, one may think of the permeability function as being controlled either by the pore pressure, p, or the effective stress, se.Many permeability functions are possible. We investigated the exponential relationship, Wyble,1 Pedrosa,2 and the power-law logarithmic relationship (Jones and Owens3 and Ostensen4). These correlations were found to be consistent with the geometric and the power-law arithmetic average respectively.
This article is a continuation of a study on stress-sensitive reservoirs published in OGJ, June 29, 1998, p. 67.5
Straight-line function
Core analysis of stress-sensitive samples is expensive because of time-consuming experiments. A common practice is to look for permeability functions in the form of straight lines. Two constants, a slope, and an intercept term characterize these straight lines.A linear relationship makes interpolation easy, and a line may be defined by only two measurements.
If more measurements are available, the two parameters may be obtained by linear regression. The quality of the approximation may be characterized by the correlation coefficient. Such calculations can be done on a hand calculator or with a spreadsheet.
Average permeability functions
An objective of conventional core analysis is to obtain an unbiased estimate of the reservoir permeability. For a pressure-sensitive reservoir, this corresponds to obtaining an unbiased estimate of the permeability function. If N cores with reference permeabilities kj* are available, the reference permeability is the permeability measured at some reference pressure, p*, or stress se*. These are arbitrary. For each core, j, the permeability function is given by Equation 2.The index n is used to denote that the permeability function has been normalized with respect to reference permeability, such as knj = kj/kj*.
The normalized permeability function for each core, j, may be assumed to be described by a permeability function of the same type. The parameter that controls the normalized permeability function, however, may vary from one core to the next.
Therefore, the objective is to seek an average permeability function, k, which is given by Equation 3, such that the average permeability function, kn, may be described by the same function as for the individual cores.
Power-law log relationship
Jones and Owens 3 investigated the behavior of stress-sensitive sandstones from low-permeability reservoirs, with more than 100 samples from five formations. They concluded that the permeability function may be described by Equation 4. In their study, they used an effective stress condition se* = 1,000 psi as a reference.Ostensen4 investigated low-permeability cores, where permeability was believed to be controlled by micro cracks. His investigation confirmed that permeability could be described by an equation similar to the one obtained by Jones and Owens.3
He recommend using the value c = 1/2 for the exponent in the power-law term rather than c = 1/3 as proposed by Jones and Owens.3 Furthermore, Ostensen pointed out that the equation may predict zero permeability prematurely. Hence, it may not be valid for large values of effective stress.
He then proposed an improved correlation that approaches zero asymptotically.
A generalized version of Jones and Owens correlation is given by Equation 5. This equation will show a straight line on a kjc vs. log(se/se*) plot. This means that linear regression is possible. The straight line is characterized by a slope, Sj, and an intercept kj*c with the log sen = 0 axisThe power-law arithmetic average may be defined by Equation 6. where the indices p and [c] denote power-law average and exponent of the Jones and Owens correlation, respectively.
The power-law average may be thought of as a generalized arithmetic average since the latter is included as a special case, such as ka = kp[c] for c = 1.
The permeability function for each core is given by Equation 5. Substituting Equation 5 into Equation 6 yields Equation 7.
The power-law average reference permeability is given by Equation 8 and the average slope by Equation 9.
In the same way as for the individual cores, Equation 5, the average power-law permeability function, Equation 10, will plot as a straight line.
Exponential relationship
According to Wyble 1 and Pedrosa, 2 permeability may be described by an exponential function of pressure changes given by Equation 12. Here, g is a constant modulus to permeability, Equation 14. Taking the logarithm of both sides of Equation 12 yields Equation 15, which will plot as a straight line for ln kj vs. Dp. It is characterized by slope Sj and intercept ln kj*.If N cores of exponential behavior are available, the geometric average is defined by Equation 16. Substituting Equation 12 into Equation 16 yields the geometric average,6 Equation 17. The indices g and a denote geometric and arithmetic averages, respectively.
Note that the geometric average permeability function will be a straight line on a plot of ln kg vs. Dp. The average slope, y, and intercept, kg* , terms are given by Equation 18 and 19, respectively.Application
The permeability obtained by well testing may be verified against average permeabilities from core analysis. An arithmetic average gives higher values than the geometric average. The power-law average will fall in between these values.An average permeability function is harder to obtain than an average number. It is difficult to associate more than one average permeability function with each permeability correlation.
The geometric average is consistent with the Wyble correlation1 and the power-law average with the Jones and Owens correlation.3 There is a possibility that both correlations may fit the case with essentially the same accuracy as measured by the correlation coefficients.7
Hence, the two average permeability functions should be compared against the well test permeability function.
Ideally, the well test permeability function should fall in the range between the power-law arithmetic and geometric averages. The power-law average permeability function may be adjusted by changing the value of exponent c. One should, however, use only the c values that lead to a high correlation coefficient for the permeability function of the individual cores.
It may be possible to obtain permeability functions by traditional well testing. Kikani and Pedrosa8 demonstrated that the dimensionless modulus to permeability may be obtained by type-curve matching. This implies that the permeability function is implicitly known.5
The natural choice for a reference pressure in well test applications is the initial pressure for a new well and the average pressure for an old one. These permeabilities may be reflected by the slope of a conventional Horner plot.9
It is important to remember that two parameter functions are approximations to a complex reality. Hence, the use of a simplified permeability function should be applied with caution for large drawdowns; however, the accuracy of the approximations improves with increasing pressure in a buildup test.
Example calculation
Jones and Owens 3 published the results from their core-analyses. We used 10 of their core results to illustrate our proposed methodology. All the samples are from the Frontier formation.Table 1 [80,436 bytes], Column 2 and 3 lists the permeability, k*, at the reference stress, and the slope term, S, respectively.
While the slope variation is rather narrow, the corresponding range for the reference permeability is substantial.
The power-law-arithmetic average is given by Equation 7. It depends on two parameters, the power-law average of the reference permeabilities and the average slope term. These are given by Equations 8 and 9, respectively.
The first step in the calculation procedure is to compute the power-law average reference permeability. Jones and Owens recommended using exponent c = 1/3 in the power-law term which corresponds to the cubic root.
The cubic root of the reference permeability of each sample is given in Column 4. Note that the range of variation is narrow.
The arithmetic average of the cubic root reference permeability is computed. This number,
The average slope term is calculated according to Equation 9. Column 5 lists the power-law permeability-slope product. The last entry of Column 5 is the arithmetic average value.
The computation is finalized by dividing the number obtained by the end results from the previous calculation, .
There is one straight line for each sample. The cubic root of the average permeability function, kw1/3p[1/3] , is displayed by the bold faced straight line on the same graph.
References
- Wyble, D.O., "Effect of Applied Pressure on the Conductive Porosity and Permeability of Sandstones," Transactions AIME 1958, Vol. 213, pp. 430-32.
- Pedrosa, O.A., "Pressure Transient Response in Stress-Sensitive Formations," Paper No. SPE 15115, SPE California Regional Meeting, Oakland, Calif., Apr. 2-4, 1986.
- Jones, F.O., and Owens, W.W., "A Laboratory Study of Gas Sands," JPT, September 1980, pp. 1631-40.
- Ostensen, R.W., "The Effect of Stress-Dependent Permeability on Gas Production and Well Testing," SPEFE, June 1986, pp. 227-35.
- Jelmert, T.A., and Selseng, H., "A Horner plot aids analysis in stress-sensitive reservoirs," OGJ, June 29 1998, p. 67.
- Jelmert, T.A., and Selseng, H., "Pressure Transient Behavior of Stress-Sensitive Reservoirs," Paper No. SPE 38970, 5th Latin American and Caribbean Conference an Exhibition, Aug. 30-Sept. 3 1997, Rio de Janeiro.
- Jelmert, T.A., and Selseng, H., "Properties Two-Parameter Permeability Functions," Forth Nordic Symposium of Petrophysics, Jan. 29-30, 1998, Gothenburg, Sweden.
- Vairogs, J., and Rhodes, V.W., "Pressure Transient Test in Formations Having Stress-Sensitive Permeability," JPT, August 1973, pp. 965-70.
- Kikani, J., and Pedrosa, O.A., "Perturbation Analysis of Stress-Sensitive Reservoirs," SPEFE, September 1991, pp. 379-86.
The Authors
Tom A. Jelmert is associate professor of petroleum engineering at the Norwegian Institute of Technology (NTH) in Trondheim. He previously was a research engineer with Sintef (Foundation for Scientific & Industrial Research at NTH) and has taught mathematics and physics at the Academy of the Royal Norwegian Air Force.Jelmert holds a BS in electrical engineering from Purdue University and an MS and PhD in petroleum engineering from NTH.
Harald Selseng is a staff engineer with Saga Petroleum ASA, Oslo. He has worked with Saga since 1986. His experience includes well test interpretation and operations, reservoir simulation studies, and production technology. Selseng has a BS in in natural gas engineering from Salford University, U.K.
Copyright 1998 Oil & Gas Journal. All Rights Reserved.