Low-resistivity beds may produce water-free
To analyze whether a zone will produce water-free from a low-resistivity formation, one can use several shaly sand models that correct log-indicated water saturations to obtain true formation water saturation.
And if low resistivity is due to micro-porosity effects, nuclear magnetic resonance (NMR) logs will indicate if the formation will produce water-free.
Low-resistivity readings can be caused by inclusion of clay or pyrite minerals and from microporosity. Clean oil-bearing sandstones have a high resistivity, but when this rock contains clay or heavy minerals such as pyrite, the resistivity can become low.
The main problem with pyrite is to estimate its volume and distribution for correcting the formation resistivity. Pyrite shows good electrical conductivity that is usually comparable to or even higher than formation water conductivity, and, therefore, it may have a larger effect on log readings than shale.
In the case of shaly formations, several models are available for correcting the water saturation. The choice of the model is controlled by the type, the distribution, and volume of clay minerals in the pay zones.
In the case of low-resistivity sands due to microporosity, evaluation of hydrocarbon potential needs logging techniques, such as NMR log, that do not depend on rock conductivity. The NMR log can determine more accurately the hydrocarbon saturation and distinguish between free water and bound water in the reservoir.
Low-resistivity sands
Low-resistivity sands can be classified into two groups:
- Reservoirs where the true water saturation is high, but water-free hydrocarbons are produced. Often, these high water-saturation readings are caused by microporosity.
- Reservoirs where the calculated water saturation is higher than the true water saturation. Conductive minerals such as clay minerals and pyrite cause the high water saturation readings.
Resistivity values, therefore, must be corrected for these conductive minerals to reduce the calculated water saturation to reasonable levels associated with water-free hydrocarbon production.
Large surface areas of certain inclusions, such as clay minerals, can cause high water-saturation readings, although other mechanisms such as high capillarity can bind large amounts of water.
In sandstones, high capillarity may be due to high-to-moderate surface clay minerals such as kaolinite or illite. But in carbonates, high-capillarity may be attributed to microporosity caused by recrystallization, dolomitization, or oolites that creates secondary porosity.1 2
Most formations logged for potential oil or gas production consist of rocks that without fluids would not conduct an electrical current. There are two types of rock conductivity:
- 1. Electrolytic conductivity, a property of water containing dissolved salts.
- 2. Electronic conductivity, a property of graphite and metal sulfides such as pyrite.
Pyrite is a common heavy mineral associated with marine sedimentary rocks. It has good electrical conductivity that is usually comparable to, or even higher than formation-water conductivity.
Pyrite crystals may form a continuous network even at low pyrite concentrations. Measured resistivity of dry pyrite ranges between 0.03 and 0.8 ohm-m.
Pyrite's conduction is of metallic (electronic) nature and consequently any transfer of current between water and pyrites is based on a conversion from ionic to electronic conduction and vise versa.
This leads to polarization at the water-pyrite interfaces with the corresponding frequency-dependent electrical properties.
Thus, the electrical properties of porous rocks with pyrites strongly depend on the amount and distribution of pyrite and the frequency of the electric current measurement.
The main problem with minerals such as pyrite is how to estimate their volume and the distribution from well logs.3 4
Clean reservoir rock conductive properties are of electrolytic origin. The presence of brine alone or mixed with hydrocarbons in the pore spaces will allow electrical current to flow. The water phase must be continuous for it to contribute to rock conductivity.
Dry minerals, with the exceptions of pyrite, hematite, graphite, and a few others, have extremely high resistivities.
Some minerals, such as clays, appear to be solid conductors.5 6
The problem of low-resistivity reservoir is not one of being able to locate the presence of hydrocarbons, but it is how to predict that little or no water will be produced even though resistivity log analyses indicate a high water saturation.
In the case of low resistivity due to microporosity, NMR logging techniques more accurately determine petrophysical properties.7
Clay minerals
Clay minerals can be classified according to the thickness of the platelets or the spacing of the crystal lattice. Most clay minerals consist of platelets of alumina-octahedron and silica-tetrahedron lattices. An excess of negative electrical charge is usually within clay platelets.
Clay found in sedimentary formations usually includes several mineral types and may be mixed with silts and carbonates in varying proportions. Their pore space will depend on the particle arrangement and on the degree of rock compaction.
These pores generally contain water but it is possible to find solid or liquid hydrocarbons or gases in them. Hence, log response to a clay depends on its composition, porosity, and hydrocarbon content.
Clay resistivity
Clays consist of thin sheet-like crystal structures, which have a large surface depending on the clay mineral type (Fig. 1). The observed deficiency of the electrical charge within the clay sheet must be compensated to maintain the electrical neutrality of the clay structure.
The compensating agents are positive ions (cations or counter ions) that cling to the surface of the clay sheets. The amount of these compensating ions constitutes the cation cxchange capacity (CEC in meq/100 g for dry rock or Qv in meq/cc for total pore volume).
CEC is related to the specific surface area of a clay mineral. Its value is least in kaolinite and greatest in montmorillonite and vermiculite. When the clay particles are immersed in water, dielectric properties of the water reduce the coulomb forces holding these positive ions.
Some of the counter ions leave the clay surface and move relatively free in a layer of water close to the crystal surface and contribute to rock conductivity. The thickness of this conductive layer expands as the solution salinity decreases. Clay conductivity is proportional to the volume of the counter ion exclusion layer.
The conductivity of clayey sediment is thus the sum of the following two terms:
- The first term is associated with free water or the water-filled porosity.
- The other term is associated with the CEC.
This can be expressed in another way. A clayey sediment has a conductivity that depends on its effective porosity on one hand and on the effective conductivity of the water it contains on the other.3 5 6
Shale models
The dispersive dielectric behavior of shaly sands is controlled by the geometry and surface area of the solid grains as well as by electrochemical processes acting on the interfaces between clays and aqueous electrolyte.5 8 9
Shaly formation resistivity depends on the shale type, shale volume, and mode of distribution in the rock.
Berg proposed that decreased resistivity caused by the dispersed clays can be associated with the matrix instead of the bound water.10 Inherent in this assumption is that formation water resistivity, Rw, in the sand pore spaces is the same as the Rw of most of the water in the clay pore spaces. This assumption might seem unusual to some, but it is justified for several reasons.
Clay, although relatively impermeable to oil and gas, has permeability with respect to water, and over geologic time the water in clay and sand pore spaces should come to equilibrium.
In addition, the amount of excess conductivity should directly depend on the amount of clay cations, which in turn directly depend on the amount of clay. Therefore, anomalous resistivity caused by the clay counter ions can be treated as a surface effect associated with the clay grains and the bound water can be treated as the far water.3
Over the last few years, a considerable number of shaly sand models relating resistivity to water saturation has been proposed. References 11-22 contain details on the shale-sand model algorithms. The effect of clays on the conductivity of mastic sediments is the subject of several petrophysical models.19
All these models consist of two terms, a clean-sand term described generally by Archie's equation and a shale term. The shale term could be fairly simple or very complicated. All models return to Archie's formula when shale volume becomes zero.
For low shale volume, the recommendation is not use these models unless the analysis requires very accurate water-saturation values.
Shale mode distribution
Log analysts customarily distinguish three modes of shale distribution: laminated shales, dispersed shales, and structured shales. Each mode has a different effect on the resistivity, spontaneous potential, porosity logs, radioactivity, permeability, and water saturation.
- Laminated shales. Laminated shales are thin beds or streaks of shale deposited between layers of reservoir rock such as sand, limestone, etc. Shales do not alter the effective porosity, saturation, or permeability of each intermediate reservoir layer, unless they form lateral permeability barriers. Shales do impede vertical permeability between porous beds.
Laminar shales can be considered to have the same properties as neighboring thick shale beds because they have been subjected to the same conditions of compaction.
- Dispersed shales. Dispersed shales adhere to the rock grains, either coating them or partially filling the pore spaces. Shaly sands with dispersed clays exhibit different properties from laminar shales because they are subjected to different constraints.
These shales in the pores markedly reduce the permeability by filling the space available for fluid movement in the pores and channels and by having a wettability in respect to water that is generally greater than quartz.
The consequences of these shales are an increase in water saturation and a reduction in fluid mobility.
- Structural shales. Structural shales form a part of the solid matrix along with quartz and other grains. These shales have many characteristics in common with laminar shales and nearby massive shales because they have been subjected to similar diagnostic depositional constraints.
Their effects on permeability and resistivity, however, are closer to those of dispersed clays.
Total shale model
In some cases, it is possible to use the following equation to calculate water saturation, Sw, independently of the distribution of shale:21 22
Sw = [aRw/(f2Rt + (aRwVsh/2f2Rsh)2]0.5 - (aRwVsh/2f2Rsh) (1)
In the equation Vsh is for total shale volume and Rsh is the resistivity of the adjacent shale bed. The Rw is formation water resistivity, f is porosity, Rt is the log resitivity, and a is a constant.
Equation 1 has been accepted widely and applied in many areas including Nigeria, Argentina, Egypt, US, and Libya. One limitation is that the porosity exponent is 2 and the value of aRw must be accurately identified.
This limitation can be overcome by including both the cementation exponent m and saturation exponent n as variables.
Patchett, Rausch model
The Patchett and Rausch model can be written as:12
Swn = (aRwRmf/Rtfm(RmfRw)Ash (2)
Ash = 1 - 10-SP/(60+0.1333T) (3)
In these equations, Rmf is the mud filtrate resistivity, T is formation temperature in °F., and SP is spontaneous potential.
One can rewrite Equation 2 as:
Log Rt/Ash = -mlog f + log aRmfRw/(Rmf - Rw) - nlog Sw (4)
Equation 4 indicates that a cross-plot of Rt/Ash vs. f (on log-log paper) should result in a straight line with a slope equal to -m, provided that a, Rw, Rmf, and Sw are constants. The intercept at 100% porosity equals aRmfRw/(Rmf - Rw).
Effective-medium resistivity model
Rock matrix and hydrocarbons can be treated together as a dispersive phase in a continuous water phase.10 The matrix grains have to be connected, whereas the hydrocarbons can be but do not need to be connected.
The connectivity, however, probably does not matter because the more resistive dispersed elements react passively to current flow in the more conductive water. The relationship between those elements can be treated as resistors in parallel, which mathematically is a volumetric weighted average conductivity.
Deriving the water saturation equation necessitated association of the matrix and hydrocarbon. The easiest part of setting up the equation is the association of water saturation with porosity.
Berg has adapted the Hanai-Bruggeman equation for rocks, as follows:10
Swf = Rw/Rt)1/m (Rt - Rd/Rw - Rd) (5) and Rd = (Rr/(1 - f)) (1 - Swf) (6)
In Equation 6, Sw is the whole rock saturation, Rt is the partially saturated whole rock resistivity, Rd is the dispersed phase resistivity (matrix and hydrocarbon ) and Rr, is the matrix resistivity.
Combining Equations 5 and 6 gives:
Sw = [-B-(B2 + 4HRm(Rt-Rm)0.5]/(2fRm)
where:
H = (Rw/Rt)1/m
Rm = Rr/ (1 - f) and
B = Rw - Rm(H + 1)
Only five input parameters (Rw, Rt, f, m, and Rr) are needed for calculating water saturation Sw. The calculation results, therefore, depend on accurate values for m and Rr because Rw, Rt, and f are usually known.
In fact, the effective medium model uses the same input as the dual-water model.
As in the dual-water model, it may be possible to refine the model by cross-plotting techniques or by improving calculation of input variables.
The desirability of this theoretical model in general is that as long as the original assumptions apply to the phenomena being studied, they should accurately describe those phenomena.
Theoretical assumptions are usually stated explicitly, while the restrictions imposed by empirical models may not readily be apparent.
The accuracy of an empirical model may decline when conditions differ from the conditions under which one derives the model.
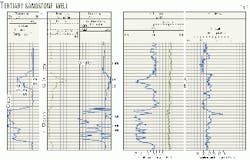
Tertiary sandstone example
The first example is for a low-resistivity pay zone in tertiary sandstones (Fig. 3). The well's logs have no short normal or SP curves because the well was drilled with oil base mud.
Water saturation in the same interval was calculated using two shaly sand models: the simplified shaly sand model and the complete shaly sand model.
The simplified shaly sand interpretation used an average value of neutron-density log readings and the Rt values from Archie's equation.
Formation water resistivity, Rw, of 0.017 ohm-m was calculated from the clean water sand, where Rt = 0.19 ohm-m (interval 10,290-10,330 ft).
From induction log data, Rt for Zone A equals 6.7 ohm-m and 2.9 ohm-m for Zone B. Shaly corrected porosity was 0.23 for Zone A and 0.19 for Zone B.
Water-saturation value, Sw, from Archie's equation, was 21.9% for Zone A and 40.3% for Zone B (Table 1).
The complete shaly sand interpretation used the following equation of Fertl and Hammack:
Sw = (FRw/Rt)0.5 - VshRw/0.4Rshf (8)
In the equation, 0.4 Rsh is clay resistivity corresponding to the adjacent shale layer and f is the porosity corrected for shale volume.
Shale volume Vsh was 14% for Zone A and 34% for Zone B. Shale values for the model were taken from the adjacent shale layer (10,180-10,200), Rsh = 0.91 ohm-m, fdsh = 0.08, and fnsh = 0.33.
With the Fertl and Hammack model, water saturation was calculated for the two zones and equals to 19.1% for Zone A and 31.9% for Zone B (Table 1).
The calculated Zone A water saturation is relatively close for both approaches, and it is recommended to use Archie's equations before spending time and effort on any shaly sand model.
But in Zone B, a shaly sand, the models produced significantly difference result.
Shaly sandstone example
Reference 17 discussed this example of a shaly sandstone formation with low resistivity using a shale-sand modeling technique developed by Schlumberger.
Fig. 4 shows SP, resistivity, neutron and density logs. In this example, the total shale model (Equation 1) was used after being modified.
The modified total shale model included a, n, and m constants together with the shale terms. The Humble equation constants were selected as follows: a = 0.62, m = 2.15, and saturation exponent n = 2.
Equation 1 after modifying it to include shale term Atsh and Btsh becomes:
Rt/Atsh = aRwf-mS-nw (9)
The total shale group Atsh is given by:
Atsh = 1 + fmRt/aRw[(2B2tsh - 2Btsh(aRw/(mRt + B2tsh)0.5] 10)
and Btsh = a RwVtsh /2fmRtsh (11)
For clean formations, Btsh becomes zero and Atsh is unity. Btsh decreases with Vsh while Atsh increases with Vsh. For a shale layer, Rt in Equations 10 will equal Rsh.
Equation 12 is obtained by taking the logarithm of both sides of Equation 9.
log Rt/Atsh = -mlog f + log(aRw) -nlog Sw (12)
Equation 12 indicates that a log-log plot of Rt/Atsh vs. f should be straight line with slope of -m, providing that aRw and Sw are constants. The resistivity index for shaly formation is calculated using the following equation:
Itsh = (Rt/Atsh)h/(Ro/Atsh)w
Water saturation Sw is derived as follows:
Sw = I-1/ntsh
From the log-log plot, it is also possible to calculate Sw with Equation 15.
Sw = (fw/fh)m/n
In this equation fw is the porosity reading on the 100% water saturation line of a Picket cross-plot,23 and fh is the porosity of the hydrocarbon bearing interval.
Table 2 lists the values of Rt, f, and Vtsh as reported by Schlumberger for this example. Also shown are values of Atsh, Btsh, and Itsh calculated by Equations 10, 11, and 13.
The last column includes values of Rt/Atsh that are cross-plotted against f on a log-log coordinate (Fig. 5).
The slope of straight line through Points 4 and 5 gives m = 2.15, while the intersection of the porosity axis at 100 % porosity gives a = 0.62. This validates the assumed values. If the straight line did not go through Points 4 and 5, new values of a and m could be assumed.
Water saturation was calculated using Equations 18 and 19. For this calculation, Rw = 0.17 ohm-m, Ro = 1.29 ohm-m, Rtsh = 1.19 ohm-m, a = 0.62, m = 2.15, and n = 2. Table 3 shows resulting water saturation values from Archie's equation, Schlumberger's program (Saraband, Coriband), and from Equations 14 and 15.
The difference between water saturation values derived from Archie's equation and other shaly sand equations indicates the importance of using a shale sand model for this example.
Also it is obvious that Schlumberger values and Picket cross-plot values are almost the same.
Previous knowledge of m and aRw is not needed for the Picket plot of the modified total shale (Equation 12). Based on the points shown on the cross-plot, these parameters can be determined by trial and error, but one still needs a nearby water section.
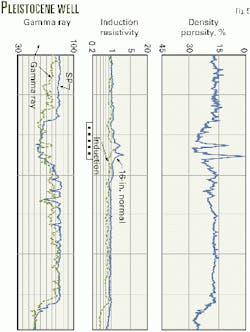
Pleistocene example
Example 3 is for a Pleistocene low-resistivity sandstone producing formation. The sandstone's low resistivity is being attributed to microporosity. It also has high capillarity caused by inclusions of moderate to high surface-area clay minerals.
In the perforated interval of a well (Fig. 6), induction resistivity is less than the shallow normal curve. This indicates that the interval is a water zone.
Log calculated water saturations (Sw) from the best shaly sand model ranged from 50 to 80%. But this well has produced oil and gas with little water, less than 0.02%.
This example demonstrates the failure of resistivity logs to locate this hydrocarbon zone or to predict little water production. NMR measurements, therefore, are needed.
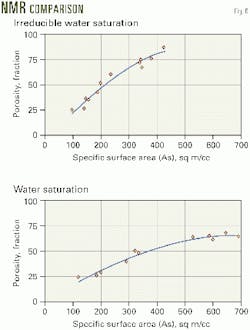
Irreducible water saturation (Swir) can be calculated from NMR measurements on sidewall core samples (Fig. 6a). Fig. 6b shows the water saturation calculated from resistivity data and density porosity. Thus, water-free hydrocarbon would be produced over the interval where Sw = Swir.
The comparison between water saturation from induction log and density porosity, and irreducible water saturation from NMR (Swir in Fig. 6a is generally greater Sw in Fig. 6b ) shows that this low-resistivity interval will produce oil with very little water.
References
- Zemanek, J., "Low- resistivity hydrocarbon bearing sand reservoir," SPE Formation Evaluation, December 1989, pp. 515-21.
- Hamada, G.M., and Al-Awad, M.N.J., "Petrophysical evaluation of low resistivity sandstone reservoirs," JCPT, Vol. 39, No. 7, 2000. pp. 7-14.
- Clavier, C., Coates, G., and Dumanoir, J., "The theoretical and experimental basis for the dual water model for the interpretation of shaly sand," JPT, Vol. 24, 1984, pp. 153-68.
- Klimentos, T., "Pyrite volume estimation by well log analysis and petrophysical studies," The Log Analyst, Vol. 36, No. 6, 1995, p. 11-17.
- Serra, O., Fundamentals of well log interpretation, Elsevier, NewYork, 1984,
- Log interpretation principles/applications, Schlumberger, NewYork, 1987.
- Hamada, G.M., Al-Blehed, M.S., and Al-Awad, M.N.J., "NMR logs find reserves by-passed by conventional analysis," OGJ, Sept. 27, 1999, pp. 75-80
- Sen, P. N., Scala, C., and Cohen, M.H., "A self similar model for sedimentary rocks with application to the di-electric constant of fiiseed glass leads," Geophysics, Vol. 46, 1981, pp. 781-95.
- Schwartz, L.M., Sen, P.N., and Johnson, D.L., "Influence of rough surfaces on electrolytic conduction," Physical Review Bulletin, Vol. 40, 1989, pp. 2450-58.
- Berg, C.R., "Effective medium resistivity models for calculating water saturation in shaly sands," The Log Analyst, Vol. 37, No. 3, 1996, pp. 16-28.
- Hossin, A., "Calcul des saturations en eau par l'methode du ciment argileux (formule d'Archie generalisee," Bulletin de L' Association des Technicienes du Petrole, 1960, p. 140.
- Patchett, J.G., and Rausch, R.W., "An approach to determining water saturation in shaly sands," JPT, Vol. 19, 1967, pp. 1395-1405.
- Tixier, M.P., Morris, P.L., and Connell, J.C., "Log-evaluation of low resistivity pay sands in the Gulf Coast," Paper E, 9th Annual Logging Symposium of SPWLA, 1968.
- Waxman, M.H., and Smits, L.J.M., "Electrical conductivities in oil bearing shaly sands," JPT, Vol. 8, 1968, pp. 107-32.
- Fertl, W.H., and Hammack, G.W., "A comparative look at water saturation computations in shaly pay sands," SPWLA Symposium 1971,
- Wiley, R. and Snoddy, M.L., "Complex resistivity of shaly sand and minerals," The Log Analyst, Vol. 28, No. 5, 1986, pp. 45-59.
- Aguilera, R., "Extensions of Pickett plots for the analysis of shaly formations by well logs," The Log Analyst, Vol. 35, No. 5, 1990, pp. 304-13.
- Hamada, G.M., "An integrated approach to determine shale and hydrocarbon potential in shaly sands," International. Symposium of the Society of Core Analysts, France, Sept. 12-14, 1996.
- Worthington, P.F., "The evolution of shaly sand concepts in reservoir evaluation," The Log Analyst, Vol. 26, 1985, pp. 23-40.
- De Kuijper, A., Sandor, R.K.J., Hofman, J.P., Koelman, J.M.V.A., Hofstra, P., and De Waal, J.A., "Electrical Conductivities in oil-bearing shaly sand accurately described with the SATORI model," The Log Analyst, Vol. 37, No. 5, 1996, pp. 22-32.
- Poupon, A., Loy, M.E., and Tixier, M.P., "A contribution to electric log Interpretation in shaly sands," AIME transactions, Vol. 201, 1954, pp. 138-45.
- Simandoux, P., "Mersures diaelectriques en milieu poreux, application a mesure des saturations en eau, etude du comportement des massifs argileux," Reveu de L'IFP, Vol. IX, 1963, pp. 193-215.
- Pickett, G.R, "Pattern recognition as a means of formation evaluation," Paper A, 14th Annual Logging Symposium SPWLA, 1973.
The authors
Musaed N.J. Al-Awad is an associate professor at King Saud University, Riyadh, Saudi Arabia. His interests are drilling engineering and petroleum-related rock mechanics. Al-Awad holds a BS and an MS in petroleum engineering from King Saud University and a PhD from Heriot-Watt University, Edinburgh.
Gharib M. Hamada is a professor of well logging and applied geophysics at King Saud University, Riyadh, Saudi Arabia. His interests are mainly in well log interpretation, formation evaluation, and reservoir geophysics. He is currently with King Saud University. Previously, he was with Cairo University, Technical University of Denmark, and Sultan Qaboos University, Oman. Hamada holds a BS and an MS in petroleum engineering from Cairo University and a DEA and a DIng in applied geophysics from Bordeaux University, France.
Mansour S. Almalik is an associate professor at King Saud University, Riyadh, Saudi Arabia. His interests are reservoir engineering, phase behavior, numerical simulation, and reserve estimates. Almalik holds a BS from King Saud University, an MS from Tulane University, New Orleans, and a PhD from Texas A&M University, College Station, Tex., all in petroleum engineering.