Method determines brine density for HPHT wells

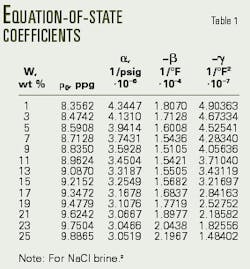
The empirical formula of Equation 1 (see equation box) accurately defines an equation of state for NaCl brines.² Table 1 presents the coefficients of Equation 1, which were generated with a multiple-regression analysis computer program, after processing laboratory density-pressure-temperature data.

Figure 1

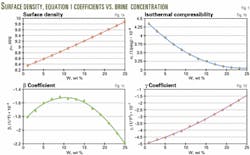
The authors also found that the coefficients of Equation 1 can be expressed accurately as second-degree polynomials (Equations 2-5, Fig. 1), directly incorporating the brine weight concentration into the equation-of-state.

Circulating temperatures

Field and analytical investigations have shown that the downhole circulating temperatures can be approximated by a linear function of depth (Equation 6).³ Equations 6 and 7 reveal that the stabilized surface outlet fluid temperature (T_out) is equal to a₀ and stabilized bottomhole brine temperature (T_bot) is expressed by Equation 7.

Workers must know the surface outlet brine temperature and bottomhole circulating brine temperature to calculate the coefficients a₀ and a₁. Mudloggers or other wellsite personnel routinely record outlet fluid circulating temperature.

One can approximate bottomhole-circulating temperature, with sufficient accuracy, using an empirical equation as a function of the geothermal gradient and bottomhole static or undisturbed temperature.^{4 5}

Hydrostatic pressure

For a static well, hydrostatic pressure of the fluid column exerts pressure at any depth, as predicted by Equation 8. With Equations 1 and 6 taken into account, integration of Equation 8 yields Equation 9.^{6 7}

Thus for given values of downhole pressure and vertical depth, engineers can estimate the brine concentration (W) required. The following example demonstrates the procedure to determine brine concentration required for a job.

Example

Sump and Williams reported that after drilling operations were completed for the 18,000-ft deep well No. 8, used for this example, the operator shut-in the well for an extended time period.⁸ Wellbore temperatures stabilized to essentially the undisturbed geothermal temperature gradient of surrounding formations.

The authors assumed T_out was 70° F. and T_bot was 412° F., bottomhole reser voir pressure was 8,500 psig, and the required overbalance was 200 psi. From the conventional formula (Equations 15 and 16), the well required a bottomhole density of 9.295 ppg.

Conventionally, one may assume that higher brine density due to increasing pressure compensates for reduced density due to increasing temperature. The wellbore average brine density of 9.295 ppg was assumed to equal the brine density at surface.

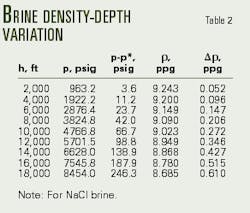
Tables 2 and 3 present the calculations of downhole pressure after application of Equations 10 and 15.

Table 2 demonstrates the importance of accounting for pressure and temperature effects on downhole brine density.

Figure 2

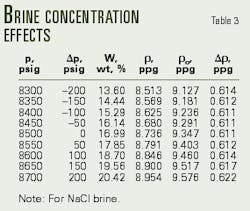
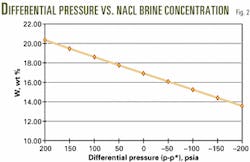
Rather than overbalanced, Table 2 reveals that the well is actually in an underbalanced condition (-46 psi). The operator must, therefore, increase the sodium chloride brine concentration from 16.20% to 20.42% (Table 3, Fig. 2).

References

1. Potter, R.W. II, and Brown, D.L., "The Volumetric Properties of Aqueous Sodium Chloride Solutions from 0° to 500° C. at Pressures up to 2,000 bars Based on a Regression of Available Data in Literature," Preliminary Tables for NaCl Solutions, Geological Survey Bulletin, Vol.1421-C, US Gov. Printing Office, Washington, 1977.
2. Kutasov, I.M., "Correlation Simplifies Obtaining Brine Density," OGJ, Aug. 5, 1991, p. 48.
3. Kutasov, I.M., "Applied Geothermics for Petroleum Engineers," Elsevier Science, New York, 1999.
4. Kutasov, I.M., and Targhi, A.K., "Better Deep-Hole BHCT Estimations Possible," OGJ, May 25, 1987, p. 71.
5. Kutasov, I.M., and Sweetman, M., "Method Predicts Equivalent Mud Density for HPHT Wells," OGJ, Sept. 24, 2001, p. 57.
6. Babu, D.R., "Effect of p-p-T Behavior of Muds on Static Presssure During Deep Well Drilling," SPE Drilling & Completion, Vol. 11, No. 2, June 1996, pp. 91-97.
7. Karstad, E., and Aadnoy, B.S., "Density Behavior of Drilling Fluids During High Pressure High Temperature Drilling Operations," Presented at the 1998 IADC/SPE Asia Pacific Drilling Conference, Jakarta, Sept. 7-9, 1998.
8. Sump, G.D., and Williams, B.B., "Prediction of Wellbore Temperatures During Mud Circulation and Cementing Operations," J. of Eng. for Industry, November 1973, pp. 1,083-92.
9. Abramowitz, M., and Stegun, I.A., "Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables," National Bureau of Standards, Math. Series 55, US Gov. Printing Office, Washington, 1972.

The authors

Izzy Kutasov is a senior lecturer in the school of petroleum engineering at University of New South Wales, Sydney. He was a graduate faculty member in the department of petroleum engineering and geosciences at Louisiana Tech University, Ruston, and worked for Shell Development Co., Houston, as a senior research physicist. He holds an MS in physics from the Yakutsk State Unversity and a PhD in physics from O. Schmidt Earth Physics Institute in Moscow. Kutasov is a member of SPE.

Tomy Seman is an undergraduate student of the school of petroleum engineering at the University of New South Wales, Sydney, and a student member of SPE.