Nonuniform loading affects casing collapse resistance
New equations developed by the Southwest Petroleum Institute, China, can calculate collapse resistance pressure for casing under nonuniform loading conditions. Click here to view Equations
This survey is in PDF format and will open in a new window
A previous article by the authors dealt with the effects of casing imperfections on collapse resistance (OGJ, Jan. 22, 2001, p. 44-47). The present article is a continuation, examining how stresses in the earth affect casing collapse resistance.
Research indicates that nonuniform loading reduces casing collapse resistance to as low as 15-30% of the collapse resistance of uniformly loaded casing. To reduce the possibility of collapse, casing design should take detrimental nonuniform loading effects into account.
Worldwide, nonuniform loading directly causes most casing collapse in wells penetrating salt formations. Directional stresses in the earth with varying degrees of maximum to minimum forces, cement channeling, creep due to salt plasticity, and casing eccentricity from the manufacturing process all contribute to the problem of nonuniform loading.
The API casing bulletin gives formulas and calculations for collapse resistance of casing under uniform loading. Little research, however, has examined the effects of nonuniform loading on casing collapse pressure. The industry has not adopted standards or algorithms to account for nonuniform loading.
Using a casing mechanical model for nonuniform loading and applying the theory of elasticity and plasticity, work done by the authors generated equations that estimate casing collapse resistance. Equation 17 calculates collapse pressure for an ideal round tube under nonuniform loading. This equation was subsequently modified to account for imperfections in the casing that occur during the manufacturing process, resulting in Equation 24.
Stress function
Once casing is run and cemented in place, the casing, cement mantle, and formation consolidate into a single structure as the cement sets-up. Stress in the system is analyzed as a plain strain problem, according to the theory of elasticity and plasticity.
The ideal casing cylinder with uniform WT is isolated from the cement mantle and analyzed separately. Equation 1 (see Equation box, Fig. 1) gives the stress function for this ideal casing cylinder.
Because the casing is a multiple-connected body, all of its displacements are single valued. The term Cr2 ln r in the stress function, therefore, must be equal zero, i.e., C0 = 0 (Equations 1 and 8).
The boundary conditions for radial and shear stress at the casing outer surface include values for the uniform and nonuniform loading forces, as indicated in Equation 5.
Equations 2-4 evaluate radial, tangential, and shear stresses at these boundary conditions. Also, the stress function coefficients A0, B0, A1, B1, C1, D1 (Equations 6-12) are determined, given the boundary conditions of Equation 5.
There are two ways to determine the casing collapse failure pressure-elastic instability and plastic yielding.2 For plastic yielding, engineers use the Von Mises Criterion in which the stress distribution is elastic up to the point of yielding. For casing sizes ranging from 5 to 95/8-in., most diameter-to-WT (D/t) ratios lie between 10 and 25. Thus, Von Mises plastic yielding shows a more representative view and will be used in the following analysis (Equation 14).
Plastic yielding first occurs at the internal wall of casing. Applying the boundary conditions of r = r1 and u = 0 into Equations 2 and 3 yields Equations 15 and 16. Then substituting Equations 15 and 16 into Equation 14 yields Equation 17, where the required coefficients are given in Equations 18-23.
Casing imperfections
Calculation of collapse resistance pressure from Equation 17 results in values that are higher than test values. Casing does not form a perfectly round cylinder but has many imperfections from the manufacturing process such as ovality, eccentricity, and residual stress.
Consideration of these imperfections requires Equation 17 to be modified to the form shown in Equation 24, before using it to calculate collapse resistance pressure.
The term PAPI is the collapse resistance pressure of casing under uniform loading when casing imperfections are taken into account. Equations 25-37 illustrate how to determine appropriate values for PAPI.3
If casing imperfections from the manufacturing process are known specifically, however, values for PAPI are calculated with the equations explained in the previous article (OGJ, Jan. 22, 2001, p. 44-47).
The nonuniformity coefficient of loading, Kp, is the ratio of minimum earth stress to maximum earth stress. Equation 24 calculates the collapse resistance of casing for all nonuniform loading scenarios.
The value of Kp is varied in the interval from 0 to 1. Thus, Equation 24 becomes applicable for both uniform and nonuniform loading.
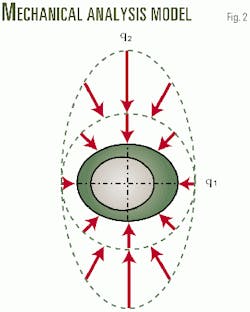
Fig. 2 is a casing cross section that shows ovality and eccentricity from manufacturing imperfections. Under uniform loading, the casing tends to collapse in the direction of maximum radius and direction of eccentricity.
Collapse resistance pressure, Pc, degrades further under nonuniform loading, if the maximum load, q2, is at right angles to the maximum radius and eccentricity.
Test data
This study employed actual 51/2-in. casing data to evaluate the validity of the equations generated. Table 1 shows the casing grades, outside diameter, and WT of casing samples used in the study.4
The distribution of elliptical loading along the outer wall of casing appears in Table 2.4 Regression analysis of the data generated maximum and minimum radius and the ratio of the elliptical loading.
Table 3 presents the collapse resistance of casing under nonuniform loading, as predicted by Equation 24, which is in excellent agreement with the actual test data.
Nonuniform loading
The nonuniform loading coefficient, Kp, ranges from 1to 0 as the maximum and minimum directional earth stress components, q1 and q2, change. For uniform loading, q2 = 0 and Kp = 1. For extreme nonuniform loading, q2 becomes very large relative to q1, and Kp = 0.
Casing collapse resistance drops as nonuniform loading becomes more severe, or as the nonuniform loading coefficient goes from 1 to 0. Fig. 3 shows the casing collapse resistance for 51/2-in. casing as loading becomes more nonuniform.
Calculated collapse resistance in Fig. 3 is given for two different grades, P-110 and N-80, and for two different wall thicknesses or casing weights. These results suggest it is more effective and practical to increase the casing WT than to use higher grades of casing.
In order to prevent casing collapse, casing design should consider the effect of nonuniform loading on casing collapse resistance.
To ensure the collapse resistance of casing, design should also consider the effects of production processes such as water injection, fracturing, acidizing, and perforating on the collapse resistance of casing.
In the case of nonuniform loading, we can adopt many technical measures to minimize collapse risk, such as partial compound casings, high collapse resistance casing, heavy wall casing, and extra-heavy wall casing.
References
- Xu Zhilun, Theory of Elasticity, People's Education Press, Beijing, 1990.
- El-Sayed, A.H., and Khalaf, F., "Resistance of Cemented Concentric Casing Strings under Non-uniform Loading," SPE 17927, SPE Drilling Engineering, March 1992.
- Bulletin on Formulas and Calculations for Casing, Tubing, Drill Pipe, and Line Pipe Properties, API Bulletin 5C3, 6th Edition, 1994.
- Wang, Zhongmao, Lu, Wanheng, and Hu, Jiangming, "Mechanism and prevention of Casing Collapse of Oil and Water Wells in Oilfield," Petroleum Industry Press, Beijing, 1994.
The authors
Han Jianzeng is in postdoctoral work at Shanghai Jiaotong University, and he is employed in the steel tube branch of Baoshan Iron & Steel Co. Ltd., Shanghai, China. His work involves research on the failure analysis of oil country tubular goods. He holds a BS, MS, and PhD in oil and gas engineering from Southwest Petroleum Institute.
Shi Taihe is a professor at the Petroleum Engineering Department in Southwest Petroleum Institute (SWPI), Nanchong City, Sichuan Province, China. His work involves research and teaching on the new technology and theory of drilling engineering. He holds a BS in drilling engineering from Petroleum Univers- ity of China and is a member of SPE.