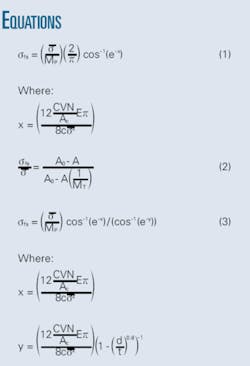
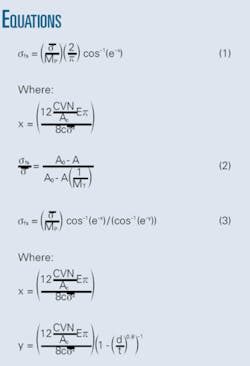
Defect Assessment—Conclusion: Modified Ln-Secant equation improves failure prediction
Limitations in the original Ln-Sec equation prompted development of a modified equation better suited thru the original equation for remaining life assessments. The modified Ln-Sec equation described in this concluding article slightly improves the failure stress prediction capability of the original. Even when including two poorly-fitting points, the modified Ln-Sec equation shows better correlation with the database of 35 full-scale experiments than the original Ln-Sec equation.
Excluding the X100 experiments yields an average ratio of actual failure stress to predicted failure stress of 1.10, with a standard deviation of 0.13. This ratio would likely exceed 0.84 in 97.5% of cases and the two poorly fitting points should be discounted.
Similar experiments appear to fit the modified model. Because it eliminates the shallow-flaw limitations of the original equation, the modified Ln-Sec equation can perform remaining life assessments for materials with sub-optimal toughness and establish flaw size following a hydrostatic pressure test in any line pipe material in common usage.
Modified equation
The usefulness of a closed-form solution for predicting defect failure pressures in pipes makes it worth having a modified Ln-Sec equation which avoids the deficiency described in Part 1 of this article. Developing an improved Ln-Sec equation would seem to entail altering the original equation so the ln-sec correction becomes defect-depth dependent. When the depth of the defect is zero, the correction should converge to a value of π/2.
Equation 1 is the original Lu-Sec equation. If corrected properly for a defect of zero depth, Equation 1 would default to Equation 2, and the predicted failure pressure for any length of zero-depth defect would be the burst pressure of the pipe. For depth-to-thickness ratios greater than zero, the inverse Ln-Sec correction should decrease from a value of π/2 at depth-WT = 0, causing only small corrections to defects with depth-WT ratios greater than 0.4.
Equation 3 would seem to do this, yielding the predicted hoop stress at failure.
Comparing the modified Ln-Sec equation to the set of full-scale experiments used to validate the original model demonstrates its validity.
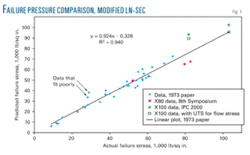
Fig. 1 shows this comparison, presenting the data reanalyzed with the modified Ln-Sec equation. Its plot has a higher R2 ratio than the plot based on the original Ln-Sec equation (0.94 vs. 0.92) and the point corresponding to the test with a notch depth-WT of 0.25 has moved much closer to the trend line (OGJ, Oct. 6, 2008, p. 78).
Points for two of the reanalyzed tests, however, moved away from the trend line on the nonconservative side. They had the lowest Charpy energies in the entire data set (about 15 ft-lb full-size-equivalent). But this may not explain their poor fit. A number of other points representing low-Charpy-energy materials fit well.
The ratios of actual-to-predicted failure stress for the two poorly fitting points measure 0.75 and 0.84. The ratios of actual-to-predicted failure stress for the other tests range from 0.88 to 1.44. Without the two poorly fitting points and the one X100 experiment, the minimum measures 0.94. These two poorly fitting points should not invalidate the modified Ln-Sec equation given that the rest of the data except for the X100 material show good correlation between predicted and actual failure stresses.
Remaining-life assessments
The modified Ln-Sec equation can calculate remaining life for longitudinally oriented defects. The method applies to corrosion, stress corrosion cracking, or any defect-growth mechanism for which growth can reasonably be assumed to be linear with time and can be estimated with reasonable certainty.
The method also can apply to growth by pressure-cycle-induced fatigue. This growth, however, is nonlinear with time and requires continuing reassessment of failure stresses as cycles accumulate. A discussion of the evaluation of pressure-cycle-fatigue-crack growth lies beyond the scope of this article.
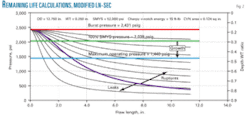
Fig. 2 shows relationships generated for 12.75-in. OD, 0.25-in WT, X52 material, assuming the material has a 15 ft-lb upper shelf Charpy energy (full-size equivalent).
The remaining defect life equals the time it takes for a defect barely surviving integrity assessment to grow to a size causing the pipe to fail at operating pressure. Representing a defect barely surviving integrity assessment as having a failure pressure of 100% SMYS is reasonable. Any larger defects would have failed in a hydrostatic test to that level or been repaired if detected by in-line inspection. If operating pressure corresponds to 72% SMYS, then the remaining life of the defect corresponds to the time it takes for a 28% reduction in failure pressure.
Fig. 2 shows the 100% SMYS pressure level as a horizontal line at 2,039 psig and the operating pressure as a horizontal line at 1,440 psig. If one assumes a given defect will grow only in depth, not length, then the vertical distance between these two horizontal lines represents the amount of growth in depth corresponding to the remaining life of the defect.
A 10-in. long defect intersects the horizontal line representing the test pressure of 2,039 psig at a depth-WT of 0.12. The horizontal line representing an operating pressure of 1,440 psig intersects a vertical line drawn at 10 in. on the length axis at a depth-WT ration of 0.36.
An arrow on Fig. 2 shows this growth. The growth of this defect equals 24% of the 0.25-in. wall thickness, or 0.06 in. If the defect grows at a rate of 6 mils/year (0.006 in./year), 60 mils of growth would take 10 years, the remaining life of the defect.
Repeating this process for defects of other lengths (2 in., 4 in., 6 in., etc.) yields the times to failure shown in the accompanying table. Remaining life stands as practically independent of defect length for defects longer than vDt and integrity assessment to 100% SMYS guarantees about 10 years. A prudent operator will, of course, prevent the remaining life from running out, instead scheduling remediation. A widely accepted practice suggests remediation when half the remaining life has expired, assuring a safety factor on remaining life of 2.