Method evaluates wellbore stimulation efficiency
A new method determines the skin factor for stimulated wells producing against constant bottomhole pressure.
Drilling, completion, and producing operations may reduce near-wellbore permeability, thereby increasing pressure loss due to skin and correspondingly reducing well productivity. This damage can be eliminated with acidizing or hydraulic fracturing that may improve the well productivity even exceediing production levels corresponding to undamaged conditions.1
To assess the damage, one can use the equations shown in the accompanying equation box.
Skin-factor calculation
If cumulative production and time data are available for a well produced against a constant pressure, then one can calculate the skin factor from the flowing time and cumulative production data.
For a well producing against a constant pressure from an infinite-acting reservoir, one can apply the concept of an effective wellbore radius.2 In this case, cumulative produced volume in oil field units is defined by Equation 1.3
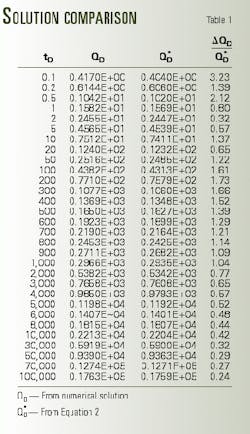
Then from Equations 2-7, one can estimate the dimensionless cumulative production.4
Table 1 compares the values of dimensionless cumulative fluid production (QD) with the results of a numerical solution.5 The table indicates that Equation 2 is valid for any production time.
Thus, from Equations 1-7, one can calculate the dimensionless production time tD. From Equation 5, one obtains Equation 8 and then Equation 9.
Example
As an example (modified from Reference 3), an oil well is producing with a constant bottomhole pressure (BHP) of 2,000 psia for 1 hr from a reservoir with a pressure of 2,500 psia. The reservoir is infinite acting and its other properties include:
If one assumes that a new test found that the formation was damaged, so that Q(t=1 hr) = 0.116 stb before stimulation and Q(t=1 hr) = 0.699 stb after stimulation, the skin (s) = 0.035, which agrees with values calculated from Table 1 data that indicate an s = 0.
In a similar manner, one can obtain s = 2.44 at Q(t=1 hr) = 0.116 stb before stimulation and an s = -2.04 after stimulation.
References
- Schechter, R.S., Oil Well Stimulation, Prentice Hall, Englewood Cliffs, NJ, 1992.
- Uraiet, A.A., and Raghavan, R., "Unsteady Flow to a Well Producing at Constant Pressure," JPT, October 1980, pp. 1803-12.
- Lee, J., Well Testing, SPE Monograph Series, 1982.
- Kutasov, I.M., Dimensionless Temperature Cumulative Heat Flow and Heat Flow Rate for a Well with a Constant Bore-face Temperature," Gothermics, Vol. 16, No. 2, pp. 467-72.
- Van Everdingen, A.F., and Hurst, W., "The Application of the Laplace Transformation to Flow Problems in Reservoirs," Transactions AIME, Vol. 186, 1949, pp. 305-24.
The author
I.M. Kutasov is senior lecturer in the school of petroleum engineering at University of New South Wales, Sydney. He was a graduate faculty member in the department of petroleum engineering and geosciences at Louisiana Tech University and worked for Shell Development Co., Houston, as a senior research physicist. Kutasov's research interests include the temperature regime of deep wells, transient pressure-flow analysis, and well drilling in permafrost areas. He holds an MS in physics from the Yakutsk State University and a PhD in physics from O. Schmidt Earth Physics Institute in Moscow. Kutasov is a member of SPE.