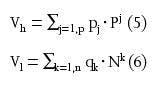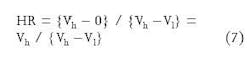Quantifying exploration back-in options using DCF method undervalues asset
Most upstream petroleum contracts provide for host countries to hold back-in rights to acquire an equity participation in resulting commercial discoveries at no exploration risk.
For reasons not arguable within the scope of this article, many oil-rich or potentially oil-rich countries' governments are cash strapped. Their cash situation could be alleviated by way of monetizing their back-in rights.
This would involve selling their rights to private investors (preferably small independent oil companies). The effective value of the deal between the oil company and the host country is determined through bargaining or via a tender. An important issue is how to value the exploration back-in option.
This article shows that the valuation of the back-in right using the traditional discounted cash flow method underestimates the asset value by at least 10%.
Introduction
Cash strapped governments or national oil companies (NOCs) that hold participating carried working interest in exploration blocks on their territory may consider issuing back-in options to be subscribed by oil companies or investors in exchange for cash.
The actual amount paid by the subscriber is determined through bargaining. Once this right is secured and included in the buyer's portfolio of exploration and production assets, an issue arises which is to determine the most appropriate measure of the value of holding the back-in option. I argue here that applying the usual risked discounted cash flow method will materially undervalue the asset (in this case the back-in right).
Oil and gas context
In most current petroleum contracts (production sharing agreement or concessions with royalty and/or tax), there is a provision that allows the government or the NOC to take a working interest up to a specified percentage at no exploration and/or development risk.
The host government's interest is usually in the form of backing into the project once a commercial discovery has been defined. Sometimes the contractor to the state concedes the provision of the later choosing to be carried through the capital-intensive development phase.
The 100% contractor borne exploration or development costs are included in a cost pool that is recovered against cost oil or as depreciation or expense for income tax calculation. Recovery each year is usually limited to a specified percentage (less than 100%) of the proportional share of revenue to which the state is entitled as a holder of a working interest in the production venture (e.g., petroleum contracts in Angola, Cameroon, Egypt, Equatorial Guinea, Gabon, Tunisia).
Each year's opening balance of nonrecovered costs bears interest usually at LIBOR plus a premium; the total amount due is carried forward for recovery the following year. Petroleum costs not recovered at the end of the commercial production life of the project are lost to the contractor.
Issues of order of recovery of petroleum costs and joint/separate recovery account(s) are very important and can be very thorny among the partnership if not agreed upon well in advance. Their impact on the individual partner's cash flow can be quite material.
Valuation framework
Consider an oil company C that has secured from an NOC x% back-in interest in an exploration block B. This option is exercisable at commercial discovery.
There are T years remaining validity for the exploration period, at the end of which an exclusive development area can be carved out and the remaining acreage relinquished by the contractor parties.
A common feature of petroleum contracts is the minimum exploration work committed (usually in the form of geological or seismic surveys and drilling of wells) by the contractor during a period of validity; this work commitment is usually coupled with a minimum financial amount that must be spent during that period.
We call E this minimum financial commitment (guaranteed by commercial bank delivered performance bond) during the exploration period. The minimum contractor's cash exposure during the exploration period is the sum of minimum financial commitment and signature bonus if any. This sum is designated Fmin.
Take r to be commercial banks' interest rate on cash deposits (e.g., LIBOR).
Geoscientists and engineers have evaluated the block and derived a probability distribution of the block's net present value (NPV) calculated at the oil company's hurdle rate of return on projects, assumed here to be its weighted average cost of capital.
The full acreage evaluation process is often multidisciplinary as required by the nature of geological, technical, and environmental challenges. The successive steps are the geological risk assessment, the volumetric estimation, the engineering support, the economic analysis and the post decision feedback.
It is not usually possible using data available when a decision on investment is required to determine the exact value of each parameter that affects the profitability of that investment. These parameters rather have a range of possible values distributed between limits that depend on the level of uncertainty or risk. This risk and the oil company's total knowledge of the investment prospect at the time of decision must be captured by the analysis.
Analysis carried out that way yields a good estimate of the value of a project as summarized by the expected monetary value (EMV) or the risk-weighted mean value of the distribution of cash-flows to be derived from the project.
We need to calculate the value of that option at the beginning of time T.
The back-in right can be assimilated to a European call option on an underlying "stock" which is x% of block B's potential oil and gas reserves.
The strike price is zero. Company C is long on this call option and will exercise its right if the expected net asset value derived from its working interest and calculated at time t = T, is positive.
The problem is to calculate the appropriate value (Vob) of the option at the beginning of the exploration period (t = 0) to be booked by the holding oil company.
For valuing the above option it is necessary to estimate the value of the exploration block/underlying stock (Vsb) at the beginning of the exploration period (t = 0).
The contractor's minimum penalty for defaulting on its contractual obligations during the exploration phase is Fmin.
Assuming that the block's contractual terms are equitable (i.e., they reflect the risk of doing business in the area, result from a competitive bid and/or bargaining process between the contractor and the state); Fmin could be used as a proxy for the value of the block to both the state and the contractor at the effective date of the contract.
To simplify the process, we shall assume that only two outcomes (success or failure) are possible at end of the current exploration period.
Success corresponds to a high (positive) asset value Vh in which case the option holder exercises its right.
Failure corresponds to a low (negative or null) asset value Vl in which case the option holder will decline to exercise the right (i.e., there is no commercial discovery resulting from the exploration of block B).
In practice discrete conditional probabilities can be assigned, with the domain of NPV, calculated at time t = T, of possible outcomes split into two ranges of ranked values corresponding to:
•p intervals of positive NPVs (Pj)j=1,p with border values NPVj (j = 1,p + 1).
•n intervals of negative NPVs (Nk)k=1,n border values NPVk (k = 1,n + 1).
Vh is the mean of a conditional (on NPV being positive) probability distribution of p positive NPVs.
Vl is the mean of a conditional (on NPV being negative or nil) probability distribution of n negative or null NPVs.
If S is the cumulative probability distribution function of possible NPVs (S-curve of NPV distribution) then
null
where Prob.(NPV<=0) is the probability of negative or nil NPVs.
At time t = T (end of the exploration period),
null
In summary we are in the presence of two virtual assets: a stock (the working interest in the exploration acreage B) and a call option (the back in right exercisable at final investment decision time T).
The future values (at t = T) of both the back-in right and the working (or equity) interest in the exploration block are uncertain.
The back-in right could be characterized as shown in Table 1.
Hedge ratio
In theory, an investor in an "efficient market" can always hedge his or her position.
An example would be to hold a stock and write options on that stock in a proportion such that at the option exercise time, the value of the combined portfolio of the stock and options does not change from what it was at the options issue time. The proportion of options to stock is called the hedge ratio.
By analogy we artificially build a hedged and virtual portfolio with the working interest on the acreage (stock) and the back-in right option.
In theory, any component of the contractor who holds a working interest in the exploration Block B could sell part of its working interest or completely farm it out at any time when the contract is still valid. The farmout, usually on a competitive basis, could be to outsiders or to remaining components (in some contracts or in the accompanying joint operating agreement, remaining partners have a right of first refusal or pre-emption in case of partial or total disposal of equity by any member of the joint venture).
The sale price must at least equal that of the most preferable outside bidder. Sometimes the government must approve the sale of interest, which is usually not a practical limitation for contenders of reputable business standing.
Although very hypothetical, a company could construct a virtually hedged portfolio through buying/holding a working interest in acreage B (long position) and issuing/writing an appropriate number of back-in options on this interest (short position).
The proportion of options to stock that would ensure a hedge (i.e. the value of the virtual portfolio is the same in the two possible exploration outcomes) at the end of the exploration period (time T) is:
null
Note that in the above equation
Vl< = 0 and thus –Vl> = 0
The hedge is (Vh – Vl) back-in options for Vh stocks.
At time T (end of exploration period), the virtual portfolio is as shown in Table 2.
The option value today
Since the virtual portfolio is perfectly hedged and thus riskless, the expected return on the hedged position should yield company C the same rate r as on a cash deposit (assume LIBOR).
At equilibrium (application of the hedge ratio and remembering that the minimum financial obligation Fmin is considered a proxy for the stock price at the beginning of the exploration period)
null
Nile Delta example
The following is an example of option versus discounted cash flow valuations of a 100% back-in right.
Assume an exploration block lying mainly offshore the Nile Delta in Egypt. Gas is the primary objective as there is a buoyant domestic market. Limited transport and processing infrastructure exists nearby and ensures fast track development and production at a maximum output of 250 MMscfd.
Contractual terms are typical of the area as they provide for a 35% maximum cost recovery and a 20%/80% profit oil split between the contractor and the government. The minimum work commitment during the 5-year validity of the current exploration period is four wells, seismic acquisition and processing at the minimum financial commitment (Fmin) of $43 million; the field abandonment provision is estimated at $20 million. No contract signature bonus is paid, and the gas price is tied via a formula to prices of Suez Blend, butane, and propane. The production condensates yield is negligible.
There are primarily two offshore exploration prospects X and Y of different sizes with geological risk ratings of 65% and 40%, respectively. In the drilling success scenarios, a three-point (25%, 50%, 25%) distribution of probable reserves is assumed. The resulting joint-distribution of possible exploration outcomes is shown in Table 3.
Valuation of back-in right
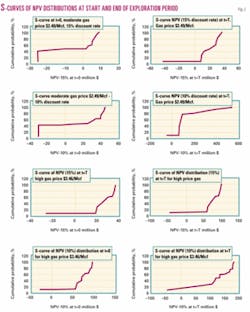
Using the assumptions described in Fig. 1 (development concept), I ran several simulations and derived the results as shown on Tables 4, 5, and 6 and graphs 1-8 of S-curves of NPV—at start and end of the exploration period—distributions (Fig. 2).
I then used these results to derive the option parameters Vh and Vl and the hedge ratio in order to compute the value of the back-in right at the beginning of the exploration period (Vob).
Vob values are then compared to the corresponding discounted cash flow method-value (Vbau) to gauge the levels of under/over valuation (Table 7).
Valuation of the option using the traditional discounted cash-flow method (Vbau or "business as usual value") sensibly underestimates the option. In the case presented here the undervaluation
null
is at least 10% (Table 7).
Bibliography
Van Horne, C.J., "Financial Management And Policy," Sixth Edition, Prentice Hall, Englewood Cliffs, NJ, 1983, pp. 85-97.
Luehrman, T.A., "A General Manager's Guide To Valuation," Harvard Business Review, May-June 1997, pp. 132-137.
The author
Manu Wope ([email protected]) is southern and eastern Africa business unit manager for Energy Africa Ltd. in Cape Town. He has a more than 18-year involvement in the international energy business at different capacities with Pecten International, SNH, World Bank, KPMG Management Consulting, and Energy Africa. He holds an MIA in economics from Columbia University, an MSc in petroleum from the French Petroleum Institute, and an MSc in electromechanical engineering from Cameroon Polytechnic School of Engineering.