Vp/Vs Crossplots identify reservoir fluids
Field examples from the Western Desert of Egypt show the effectiveness of compressional-wave velocity (Vp) and shear-wave velocity (Vs) crossplots for identifying the type of fluid contained in a formation.
Vp/Vs crossplots can distinguish between water, oil, and gas-saturated zones and therefore provide an additional tool for identifying fluids, especially in formations with little history.
The industry uses sonic travel time of a compressional wave as a tool for determining formation porosity, while the shear-wave travel time helps determine the mechanical rock properties.
A compressional wave also is sensitive to the type of fluid saturating the pore space. But the fact that compressional-wave velocity decreases and shear-wave velocity increases with the increase in light hydrocarbon saturation, makes the ratio of Vp/Vs a more sensitive indicator of fluid type than Vp or Vs used separately.
Wave properties
In the acoustic sense, the properties that define seismic-wave velocity are the elasticity parameter, E, and density, ρ.
The basic equation is V = (E/ρ)0.5. Elementary observations tell us that a sonic wave in dense rocks tends to have a high velocity.
This signifies that the effect of elasticity on velocity is much greater than the effect of density.
Because there are several moduli of elasticity, one has to select the appropriate modulus to calculate the seismic velocity. The three elastic moduli involved are:
1. Young's modules, E.
2. Bulk modulus, K.
3. Rigidity modulus, μ.
For the compressional wave (P-wave), the appropriate value of E is K + 4/3 μ or λ + 2μ, while for the shear wave (S-wave) the appropriate value of E is μ.1-4 The λ is Lame's constant.
P-wave transit-time data are useful in identifying lithology, porosity, and the fluid in the pores. S-wave data are useful for identifying minerals, porosity, and possibly fluids. The combination of S-wave and P-wave data helps identify fluid type, especially in gas reservoirs.
Factors affecting velocity
Formation porosity is an important factor in determining the velocity of seismic waves through the rock.
The Wyllie equation, Equation 1 (see Equation box) is often used to relate the velocity, V, and porosity, φ. It assumes that the travel time per unit path length in fluid-filled porous rock is the average of the travel time per unit path length in the matrix 1/Vm and in the fluid 1/Vf.
In the equation, V is seismic wave velocity, Vf is fluid velocity, and φ is effective formation porosity.
Rock density affects seismic-wave velocity; therefore, both the S and P-waves have higher velocities in denser rock. Denser rock indicates higher rock compaction, a greater depth, and higher overburden pressure.
An empirical formula relating velocity and density has the form ρ = 0.23V0.25, in which the density units are in g/cc.
The saturating fluids also affect seismic-wave velocity. This velocity is slower in gas-saturated zones compared to water or oil zones.
Seismic waves
Seismic waves have several characteristic features.5 6
The particle motion associated with P-waves consists of alternating compressions and rarefactions during which adjacent solid particles are closer together and farther apart during successive half cycles. The particle motion is always in the direction of wave propagation.
The distance between two rarefactions or compressions is known as wavelength or period
Equation 2 expresses the relation between compressional-wave velocity, Vp, density, ρ, and elastic constants. In the equation, Vp is the compressional wave velocity, E is Young's modulus, σ is Poisson's ratio, λ is Lame's constant, μ is the rigidity modulus, and ρ is rock density.
When shear deformation propagates in an elastic solid, the motion of individual particles is always perpendicular to the direction of wave propagation. Equations 3 and 4 are expressions for calculating the shear-wave velocity, Vs.
Vp/Vs combination
Equation 5 expresses the ratio of compressional to shear-wave velocity. In the equation, K is the bulk modulus of rock.
Values of Poisson's ratio s vary from 0.0 to 1.0.
Either expression indicates that the compressional-wave velocity will always be greater than the shear-wave velocity in a given medium. If σ is 0.25, the Vp/Vs ratio equals 30.5. It is worth noting that for most consolidated rock materials, Vp/Vs is between 1.5 and 2 and s is between 0.1 and 0.33.
The Vp/Vs ratio for sandstones ranges from 1.66 to 1.81 and for carbonates, 1.81 to 1.98.
Because liquids (μ = 0) do not sustain shear-wave deformation, shear waves will not propagate in liquid material. Otherwise, Equations 3-5 show that Vp is greater than Vs in a given medium. Both parameters must be greater than one. The first because K and m are always positive and the second because s cannot be greater than 0.5 in an ideal solid.7-12
Velocity equations make clear that a rigidity modulus affects shear wave velocity more than compressional wave velocity.
For P-waves, Equation 1 can take form of Equation 6 or Equation 7, where Δtp is P-wave transit time and Δts is S-wave transit time.
Seismic velocity (Vp or Vs) in Equations 6-9 is a function of three variables; fluid velocity, Vf, porosity, φ, and matrix velocity, Vm. Solution of any of these equations for one variable requires one to know the value of the other two.
One can solve Equations 7 or 9 for porosity by assuming a known fluid velocity and matrix velocity. In a hydrocarbon reservoir, such derived porosity needs to be corrected for hydrocarbon content.
In a gas reservoir, it is recommended to obtain the porosity from a density log rather than from a sonic log.
Fluid identification
If one knows or assumes a porosity and matrix velocity, one can solve Equations 6-9 for fluid velocity instead of formation porosity. P-wave velocity in water is greater than in oil or in gas. Consequently recorded P-wave velocity is sensitive to fluid change from water to oil or gas.
From velocity Equations 2 and 3, it is clear that S-wave velocity is more sensitive than the P-wave to fluid type. This sensitivity difference is attributed to the fact that the S-wave depends mainly on the rigidity modulus, μ, while Vp depends on both λ and μ.
The combination of the shear wave and compressional-wave velocities will produce a new parameter, Vp/Vs. This parameter is more sensitive to the fluid than the P or S-wave alone.
Table 1 lists the travel time, Δt, for the S and P-waves in common reservoir rocks. The Vp-Vs crossplot uses these matrix constants.
Observations show that light hydrocarbon saturation decreases the velocity of compressional wave and increases the velocity of shear wave through porous rocks, relative to formation water saturation.
Both rock density and elasticity affect the shear or compressional wave. There is a smooth decrease of density when light hydrocarbons or gas replace water in the pores. Elasticity, however, is different. The presence of some water minimally affects the ease with which the solid material can deform into the pore, but gas in the pores readily absorbs all deformation (expressed by μ). This is true whether the pores have a water saturation of 10%, 40%, or 70%. The remaining gas absorbs the deformation.
Over this range of water saturation, therefore, the elasticity remains substantially constant, while the density decreases. It follows the shear velocity increases at greater gas saturations.
When the water saturation approaches 100%, the velocity must rise considerably because no gas is left to absorb rock deformation and the water resists the deformation. All change between gas saturated velocities and water saturated velocities, therefore occur with the first bubble of free gas within the pore.
The fact that the change in size and pore deformation affects the compressional wave leads to the fact that the replacement of water by gas will decrease density and also elasticity (change in size, bulk modulus K, deformation, and shear modulus μ). The gas will only absorb the deformation, which causes a decrease in compressional-wave velocity.
When gas saturation reaches residual gas saturation and the water becomes the main fluid, the pores contain no gas free to absorb deformation. At this point the shear-wave velocity will increase suddenly. The compressional-wave velocity, on the other hand, will be affected only slightly and will keep the same increasing trend at greater water saturation
It is preferable to use Δtp-Δts in the crossplot rather than Vp-Vs. This is technically easier because these values are obtained directly from records.
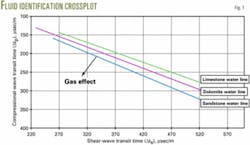
Fig. 1 shows an example of the plot in which the units of Vp/Vs are in msec/m.
The plot shows the limestone water base line, dolomite water base line, and sandstone water base line.
For a specific case such as a sandstone line, water points are those points lying on the sandstone line or above (in case of rf > 1 g/cc). Points below the sandstone line are oil or gas points.
Light hydrocarbon or gas will cause a decrease in shear-wave travel time and an increase in compressional-wave travel time with respect to the water point. This will shift the water points to the left lower corner of the crossplot, defined as the gas arrow effect in the crossplot.
Gas points will show more departure from the sandstone water base line than oil points and have more of a shift to the left and greater shear travel times.
One can apply this technique also for limestone or dolomite reservoir rocks
Field examples
Examples from the Western Desert show the application of the crossplot for identifying formation fluids.
The first example (Fig. 2a) shows the Vp-Vs crossplot for Unit 5 in a gas producing well.
The points shown in Fig. 2a indicate clearly that Zone D18 is a gas zone, whereas in Fig. 2b, Zone JB 173 is clearly a water zone.
Another example (Figs. 2c and 2d) shows that Unit 2 and U3-1 are gas while Unit 3-2 is water. Fig. 2c indicates a gas zone because the points fall below the water line and are shifted to the left.
A water zone is indicated in Fig. 2 because the points are shifted to the right and are closer to the water line.
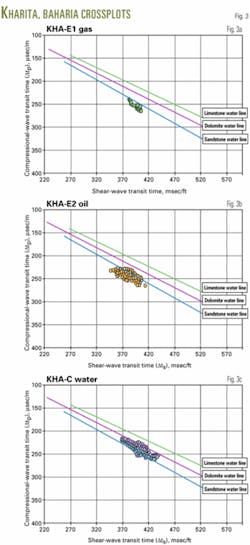
The third example (Figs. 3a and 3b) is from the Kharita formation. Fig. 3a indicates that Zone E1 and JG2 are gas zones because the points lie below the line.
Fig. 3b shows the oil zone in the well because these points lie also below the line but are shifted with respect to the gas zone points. The shift is due to the fact that oil has a different effect on the shear wave than gas.
Fig. 4 is Vp-Vs crossplot in water section of the Bahariya formation.
References
1. Anstey, N.A., Seismic interpretation: The physical aspects, IHRDC, Boston, 1977.
2. Cardona, R., Batzle, M., and Davis, T.L., "Shear waves velocity dependence on fluid saturation," SEC Annual Meeting Transaction, 2001.
3. Dominco, S.N., "Effect of brine-gas mixture on velocity in a unconsolidated sands reservoir," Geophysics, Vol. 41, 1976, pp. 882-94.
4. Ferguson, R.J., and Stewart, R.R., "Reservoir indication using Vp/Vs value derived from broadband 3C seismic data," SEG Annual Meeting, Tulsa, 1996.
5. Johnston, J.E., and Christenson, N.I., "Compressional to shear velocity ratios in sedimentary rocks," International Journal of Rocks Mechanics, Mining Sciences and Geomechanics Abstracts, Vol. 20 (1993), No. 7, pp. 751-54.
6. Klimontos, T., "Attenuation of P and S-waves as method of distinguishing gas and condensate from oil and water," Geophysics, Vol. 60, pp. 447-58.
7. Othman, A.A., and Hamada, G.M., "Acoustic properties as function of depth in the Gulf of Suez, Egypt," Petroleum Research Journal, Libya, Vol. 3 (1996), pp. 27-34.
8. Sinha, B.K., and Plana, T.J., "Wave propagation in rocks with elastic–Plastic deformation," Geophysics, Vol. 66 (2001), No. 3, pp. 772-785.
9. Soudra, W.W., "Using sonic logs to predict fluid type," Petrophysics Journal., Vol. 43 (2002), No. 5, pp. 412-19.
10. Sun, X., et al., "P and S-wave attenuation logs from monopole sonic data," Geophysics, Vol. 65 (2000), pp. 755-65.
11. Robertson, J.D., "Carbonate porosity from S/P travel time ratios, Expanded abstract," 53rd Intl. Soc. Expl. Geophysics Meeting, 1983, pp. 356-58.
12. Robertson, J.D., and Pritchett, W.C., "Direct hydrocarbon detection using Comparative P-wave and S-wave seismic sections," Geophysics, Vol. 50 (1985), pp. 383-93.
The author
Gharib M. Hamada ([email protected]) is a professor of well logging and applied geophysics at Cairo University, Egypt. Previously he was with King Saud University, Riyadh, Technical University of Denmark, Copenhagen, and Sultan Qaboos University, Muscat. His research interests are well logging data analysis, seismic modeling, and reservoir description. Hamada holds a BS and an MS in petroleum engineering from Cairo University and a DEA and a Doc. D'Ing. from Bordeaux University, France. He is a member of SPE and SPWLA.