New model forecasts natural fracture width
Hao Peng
Qian Li
Hu Yin
Petroleum and Natural Gas Engineering Institute
Southwest Petroleum University, Chengdu, China
Pu Liu
Fuling Shale Gas Development
Chongqing, China
A new model can predict fracture widths quickly in the field based on logged well data and adaptations of existing models. Operators experiencing drilling mud loss through natural fractures must accurately calculate fracture width to ensure successful plugging.
The new model outlined in this article can reduce the possibility of human error and improve calculation speed. The authors started with a mathematical model developed by Reza Majidi of the University of Tulsa based on yield-power-law (YPL) fluids.
Researchers tested the new model on fracture-related circulation loss for DaShen 001-XI well, drilled by Southwest Oil and Sichuan Northwest Gas Mine. DaShen 001-X1 is in the latent structure of Sichuan basin, Daxing field. Its design depth is 6,281 m. Circulation loss occurred at 2,821 m in the LaiKouPo layer. Lithology is limestone with fracture development. Wellbore size was 311.1 mm, bottom pressure was 4.2 MPa, drilling mud yield was 5.62 Pa, and the flow behavior index was 0.65.
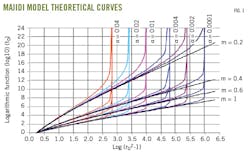
Different flow behavior indices correspond with different theoretical curves. Each theoretical curve has a unique straight-line segment which can be processed linearly. Majidi's model demonstrated drilling and theoretical curves have similar straight-line segments with linear coefficients as high as 0.999.
Researchers devised a method of least squares while developing a computational model to determine a straight-line segment based on drilling logs for leaking fluid. An adaptive search matched the drilling curve with the closest theoretical curve. A dimensionless mud-invasion coefficient enables researchers to estimate a natural fracture's width.
The new fracture-width method automatically matched drilling curves with theoretical curves. Relative error was under 0.001%.
Fluid mechanics
The ability to predict natural fracture width is essential for plugging fracture-induced circulation loss.1-2 Image logs help engineers identify whether a fracture is natural or induced by hydraulic fracturing.3-4 But image logs provide localized information, often unsuitable for engineers responding to lost circulation.
For decades, researchers have used fluid mechanics to determine drilling fluid loss in natural fractures.5-13
Olivier Lietard11 used the Bingham fluid model to develop a model for calculating natural fracture widths using logging while drilling (LWD) data. Francesca Verga12 validated hydraulic fracture widths using mud loss data and fracture electrical aperture values from image logs.
Majidi extended Lietard's model by applying YPL to drilling mud.13 Both Majidi and Lietard matched theoretical curves and corresponding actual drilling curves. Majidi manually matched the curves, but the process is cumbersome, inconvenient, and subject to error.
The new method discussed in this article combined a numerical method with an adaptive search, enabling automatic matching of theoretical curves. Adaptive search improved the new model's precision compared with Majidi's model.
Mathematical modeling
Equation 1 shows the constitutive equation for YPL. Equation 2 shows the pressure gradient. Equation 3 integrates Equation 2 to obtain wellbore pressure and initial formation pressure, resulting in Equation 4. Equation 5 shows temporal rates of change for the total loss volume.
The mud-front location is determined by combining horizontal and vertical projections of leaking drilling fluid. The mud front moves with time. Geometric relationships influence drilling fluid's invasion speed into natural fractures.
Equation 6 shows the mud front's rate of change, calculated by combining Equations 4 and 5. Equations 7-11 define various dimensionless variables: dimensionless radius, dimensionless volume, dimensionless mud-invasion coefficient, and dimensionless time.
Three parameters: α, m, and rD, determine Equation 11.
Analysis of Equations 12-13 shows each drilling curve has one corresponding theoretical curve. In matching the two, a drillng curve is shifted horizontally and vertically relative to its corresponding theoretical curve.
Natural fracture width can be calculated based on a dimensionless mud-invasion coefficient.
Fig. 1 shows a set of theoretical curves used to determine a flow behavior index as created by Majidi.
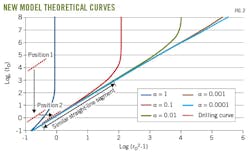
Fig. 2 shows horizontal and vertical coordinates. If a drilling curve is at Position 1, it must be moved horizontally to the right until a corresponding theoretical curve is met, enabling calculation of the natural fracture width.
Curve-matching process
Researchers draw theoretical curves for a specific well's mud rheology. They also use logged data for well leakage to draw a drilling curve for that well. The drilling curve is shifted to match the corresponding theoretical curve before calculating the natural fracture's width.
Theoretical curves can be drawn at a certain α step. It's possible for the theoretical curve to be in the blind area when matching it with a drilling curve.
For Fig. 2, the real curve matches the theoretical curve at α = 0.6, although this is not shown. After translation, the drilling curve will be between the two theoretical curves with α = 1 and α = 0.1, respectively.
The corresponding theoretical curve is estimated manually in this case, which introduces human error. As researchers shift a drill curve to fall between two theoretical curves, the chart resolution can be increased by using smaller α steps. Theoretical curves can be encrypted to minimize human error.
This approach, however, does not eliminate human error risk because theoretical curves cannot be encrypted with infinite accuracy. There always will be a drilling curve that does not precisely match its corresponding theoretical curve.
Equation 6 shows that regardless of the values of m and α, all theoretical curves have the same shape distribution and similar straight-line segments.
Researchers, trying to analyze the degree of linear correlation between similar straight-line segments, used linear correlation coefficients.
All linear correlation coefficients were found to be close to 0.999. Fig. 2 shows the slopes of the corresponding segments were 2.6437, 2.0258, 1.6210, 1.4093, and 1.3585.
Similar straight-line segments are linearly correlated. Then, for a given m, the α step automatically is determined using the adaptive search method. The slopes of similar straight-line segments for all α can be calculated.
Data for a similar straight-line segment of the drilling curve enable its slope to be calculated using least squares. Researchers compare both slopes until the relative error is within 0.001%, match the theoretical curve with the corresponding slope, and calculate the natural fracture's width.
The calculation steps are:
• Input basic parameters and set the relative error of matching.
• Calculate slopes for the set of theoretical curves with given m.
• Obtain horizontal and vertical coordinate sequences for the drilling curve.
• Establish normal equations as shown in Equation 14.
• Obtain input data. Equations 15-17 show the calculations.
• Solve Equation 18.
• Calculate linear correlation coefficient as shown in Equation 19.
• Set the α step size and the bounds.
• Establish the slope of similar straight-line segments for all values of α.
• Calculate relative percentage of error. Equation 20 shows this step.
• Determine the natural fracture' width until satisfying Equation 21, otherwise reset the α step size and the bounds.
Application example
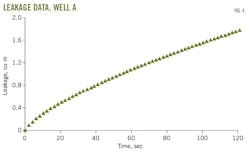
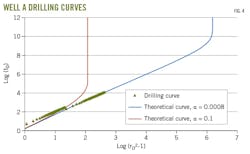
Fig. 3 shows Well A data. Using the new method on the log data, the authors specified the basic parameters. Relative error was set as the authors calculated slope of the straight-line segment for this real curve at 1.39757. The adaptive search method yielded α = 0.0008 as the corresponding theoretical curve. Authors calculated the natural fracture's width as 725 μm. To validate the findings, they translated the drilling curve's horizontal and vertical coordinate sequences.
Fig. 4 validated that the drilling curve matches the theoretical curve, confirming the correctness of the calculations. The necessary plugging material was configured accordingly to ensure a successful plugging operation.
Acknowledgment
The authors acknowledge the support of the National Science and Technology Major Project (2016ZX05020-006).
References:
1. Daqi, L., Yili, K., and Yijin, Z., "Dynamic Variation of Fracture Width and its Effects on Drilling Fluid Lost Circulation in Fractured Vuggy Reservoirs," Journal of China University of Petroleum, May 2011, pp. 76-81.
2. Yezhong, W., Yili, K., and Lijun, Y., "Progress in Mechanism Study and Control: Mud Losses to Fractured Reservoirs," Drilling Fluid & Completion Fluid, April 2007, pp. 74-77.
3. Luthi, S., and Souhaite, P, "Fracture Apertures from Electrical Borehole Scans," Society of Exploration Geophysicists', Geophysics, July 1, 1990, Vol. 55, No. 7, pp. 821-833.
4. Hornby, B., Johnson, D., Winkler, K., and Plumb, R., "Fracture Evaluation Using Reflected Stoneley-Wave Arrivals," Geophysics, Oct. 1, 1989, Vol. 54, No. 10, pp. 1274-1288.
5. Lavrov, A., "Flow of Truncated Power-Law Fluid Between Parallel Walls for Hydraulic Fracturing Applications," Journal of Non-Newtonian Fluid Mechanics, September 2015, Vol. 223, No. 9, pp. 141-146.
6. Omosebi, A., and Adenuga, K., "Pressure Drop Versus Flow Rate Profiles for Power-Law and Herschel-Bulkley Fluids," SPE Nigeria Annual International Conference and Exhibition, Lagos, Aug. 6-8, 2012.
7. Majidi, R., Miska, S., and Zhang, J., "Fingerprint of Mud Losses into Natural and Induced Fractures," SPE European Formation Damage Conference, Noordwijk, The Netherlands, June 7-10, 2011.
8. Lavrov, A., and Tronvoll, J., "Numerical Analysis of Radial Flow in a Natural Fracture: Applications in Drilling Performance and Reservoir Characterization," SPE Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, Nov. 5-8, 2006.
9. Lietard, O., and Spivey, J., "Revisiting Pressure Transient Testing of Hydraulically Fractured Wells: A Single, Simple, and Exact Analytical Solution Covering Bilinear, Linear, and Transition in Between Flow Regimes," SPE Hydraulic Fracturing Technology Conference, Jan. 24-26, 2011, The Woodlands, Tex.
10. Daqi, L., Yili, K., Xiushan, L., Zengwei, C., and Na, S., "Progress in drilling fluid loss dynamics model for fractured formations," Petroleum Drilling Techniques, July-August 2013, pp. 42-47.
11. Lietard, O., Unwin, T., and Guillot, D., "Fracture Width LWD and Drilling Mud/LCM selection guidelines," SPE European Petroleum Conference, Oct. 22-24, 1996, Milan.
12. Verga, F., Carugo, C., Chelini, V., and Maglione, R., "Detection and Characterization of Fractures in Naturally Fractured Reservoirs," SPE Annual Technical Conference and Exhibition. Oct. 1-4, 2000, Dallas.
13. Majidi, R., Miska, S., Ahmed, R., Yu, M., and Thompson, L., "Radial Flow of Yield-Power-Law Fluids: Numerical Analysis, Experimental study, and the Application for Drilling Fluid Losses in Fractured Formations," Journal of Petroleum Science and Engineering, February 2010, Vol. 70, No. 3-4, pp. 334-343.
The authors
Hao Peng ([email protected]) is a PhD student at Southwest Petroleum University. He holds an MS (2016) in petroleum engineering from the same university. His research primarily concentrates on leaking wells.
Qian Li ([email protected]) is a Southwest Petroleum University professor and doctoral tutor in oil and gas well engineering. His research focuses on deep drilling and horizontal well completions.
Hu Yin ([email protected]) is a Southwest Petroleum University associate professor in oil and gas well engineering. He studies rock mechanics, wellbore stability, complex deep wells, and ultradeep drilling.
Pu Liu ([email protected]) is a drilling engineer for Fuling Shale Gas Development working in the Chongqing Environmental Protection Research and Technical Service Center. He received a PhD from Southwest Petroleum University. He specializes in well control technology and managed pressure drilling.