New study characterizes heterogeneity in Egypt's Upper Bahariya reservoir
Abdelwahab Bayoumi
Elsayed Gomaa
Al-Azhar University
Cairo
Abdelnaser Hamdy
Khalda Petroleum Co.
Cairo
The high degree of heterogeneity in the Upper Bahariya, one of the more productive zones in Egypt's western desert, makes accurate characterization difficult. This article applies a range of reservoir characterization techniques to determine a Dykstra-Parsons coefficient (permeability variation factor) of 0.86 and a Lorenz coefficient of 0.92 for the Upper Bahariya, which confirm the formation's heterogeneity while providing insight to the reservoir's hydraulic flow, relative permeability, and water saturation.
Accurate reservoir characterization is vital in estimating recoverable oil. Permeability and porosity are the two most important parameters in evaluating a formation and describing the reservoir. Beyond evaluating these characteristics, a combination of two or more rock properties can provide insight into flow dynamics through porous media. The Leverett J-function and the reservoir quality index (RQI) are two common methods for reservoir characterization. Both methods incorporate permeability and porosity into a single quantity that serves to characterize the formation.1 Core data provides the basis for these methods along with openhole logging, pressure-volume-temperature analysis, and pressure data.
Upper Bahariya characterization
The study underlying this article relied on well correlation, hydraulic flow unit (HFU) data, and relative and capillary pressure to determine the Dykstra-Parsons and Lorenz coefficients. The results are divisible within the pressure readings and openhole logging data. The Upper Bahariya is divided into nine HFUs. Relative permeability curves show the Upper Bahariya to be a water-wet system, while capillary pressure curves show transition zones by their high heterogeneity and connate water saturation.
The formation's heterogeneity results in a poor relationship between permeability and porosity, which have a 0.3076 correlation coefficient. The capillary pressure curve shows a displacement of 15 psia (absolute pressure) within the reservoir.
Openhole logging shows the reservoir consists of thin sand layers interbedded with shales, silt, and limestone. In some areas, pressure targets suggest that reservoirs are connected and could benefit from effective waterflood programs. Pressure data also provided different decline curves in all wells, indicating reservoir compartmentalization.
Heterogeneity identification
Dykstra-Parsons and Lorenz coefficients are common static measurements that identify a reservoir's vertical heterogeneity. Heterogeneity describes permeability distribution of a given sample from the formation.2 3
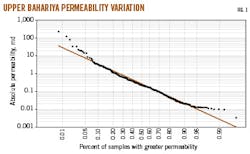
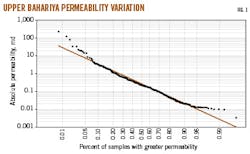
This study calculated the Dykstra-Parsons coefficient using 243 conventional core data samples from five wells. Researchers arranged core samples by decreasing permeability after removing erratic data, calculating the percentage of samples that had greater permeability than the respective samples. The straight line in Fig. 1 represents plotted permeability values against the percent of samples on the probability scale. This calculation determined corresponding permeability values at 84.1% with 50% of samples from the log-probability graph. Equation 1 calculates the permeability variation factor (VDP).
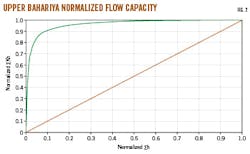
For the Lorenz coefficient, researchers arranged permeability values in descending order, calculating the dimensionless cumulative permeability and capacity.3-6 8 Fig. 2 shows the normalized and plotted data. Equation 2 calculated the Lorenz coefficient.
Well correlation, pressure data
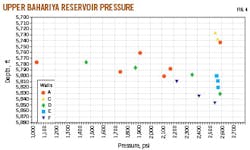
Well correlation and pressure data confirmed the reservoir's heterogeneity and continuity, indicating its thin, interbedded sand layers (Fig. 3). Log correlations are difficult in some areas and sands appear to be discontinuous. Pressure uniformity, however, suggests that the reservoirs are in fact connected. In contrast, other areas where porous sands can be easily correlated show large pressure variations, suggesting reservoir discontinuity or reduced lateral permeability. This variation across the reservoir highlights the importance of pressure data, which can provide information on reservoir continuity and determine the effectiveness of waterflood programs.
Pressures plotted as well-to-well profile comparisons provide a striking variation, both laterally and vertically (Fig. 4).
The Upper Bahariya's variation in permeability values obtained from conventional core analysis and Dykstra-Parsons and Lorenz coefficients, combined with well correlation and pressure data, indicate an extremely heterogeneous reservoir. This heterogeneity signifies that thin vertical shale barriers may or may not extend across the field and ensures an imperfect relationship between porosity values (measured and calculated) and permeability.
Permeability, porosity
Permeability depends on pore space continuity, whereas porosity signifies pore space availability. High porosity is possible without having any permeability and vice versa. Permeability defines the quality of a hydrocarbon-bearing formation.
There is no theoretical relationship between porosity and permeability in natural porous systems, and practical relationships represent a best fit often relying on a convenient mathematical relationship.
A straight line is the easiest relationship to test, and plotting porosity against the permeability logarithm leads to an approximate straight line.
Porosity is a logging parameter where permeability is not. Researchers frequently attempt to empirically correlate porosity with permeability to remove permeability as a function of depth. Downhole permeability is mainly obtained by flow and pressure determination and requires knowledge of characteristics such as the flowing interval.6 9
Reservoir heterogeneity shows little correlation between core porosity and core permeability, underlining the lack of reliable relationship between them (Fig. 5). Consequently, conventional rock-property averaging techniques (arithmetic, geometric, and harmonic) cannot be applied to determine a relationship. The only way to establish a correlation between reservoir permeability and porosity is to split the reservoir into HFUs.
Hydraulic flow units
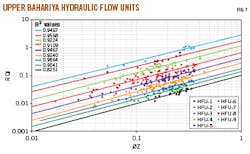
Researchers characterized the Upper Bahariya reservoir's HFUs with conventional core data (Kh and Ø) from five wells.4 10-15 The study removed fractured samples, including samples with high permeability and low porosity. Equations 3-5 calculated the RQI, normalized porosity (Øz) and the flow zone indicator (FZI).16 Researchers then arranged FZI values in ascending order and plotted RQI vs. Øz on the logarithmic scale (Fig. 6).
Determining the number of HFUs used three independent methods. The log-log plot of RQI vs. Øz is a simple analysis, but is insufficient for distinguishing rock types and their boundaries within a given HFU. Samples with similar FZI values lie on a straight line with slope = 1 (Fig. 6). Samples lying on the same straight line have similar pore throat attributes and constitute a single HFU. The mean value of FZI is indicated at the intercept of the unit slope and the straight line where Øz = 1.
FZI distribution is a superposition of multiple log-normal distributions. FZI histogram analysis defines the number of normal distributions (n) for the number of HFUs (Fig. 7).
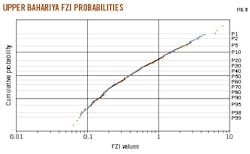
The probability plot or cumulative distribution function is the integral part of the histogram (probability density function). A normal distribution forms a straight line on a probability plot. The number of straight lines in the probability plot indicate the number of HFUs in the reservoir. This plot is smoother than a histogram and is therefore more useful in defining HFUs because cluster identification is easier (Fig. 8).
All three of these methods identified at least nine HFUs and estimated FZI boundaries for each rock type (Table 1). The value of intercept HFUs and lines at Øz = 1 is the mean FZI, determination of which further helped calculate permeability. As a final step, Equation 6 calculated permeability (K) for each HFU.16
Fig. 9 shows permeability calculations plotted against measured core permeability. The plot shows the closeness of data to the 45° straight line, indicating an accurate permeability calculation in the cross-plot. Equation 7 calculated an average relative error (ARE) of 1.4% for the estimated permeability values.
Relative permeability
Within certain fluid phases, relative permeability is the ratio of a fluid's effective permeability to the absolute permeability of rock.4 5 Relative permeability varies between 0 and 1 and is crucial in understanding multiphase fluid flow in a reservoir and in predicting future reservoir performance. Knowledge of relative permeability trends is important when undesirable water or gas flow is anticipated in an oil reservoir. A fluid phase's relative permeability is a function of the saturations of all fluid phases present in the rock. Reservoir fluids' relative permeability characteristics usually change from one location to another. Various reservoir rock facies may exhibit different relative permeability trends.
Relative permeability data are incorporated into reservoir models to make realistic predictions of recovery. The relative permeability of a certain fluid increases with the saturation of that phase in porous media. The relationship between the two parameters is nonlinear. Relative permeability serves as a common standard in reservoir studies regardless of the magnitude of the effective permeability in a reservoir.
Normalizing, averaging
Relative permeability data must be normalized to remove the effect of different initial water and critical oil saturations.4 Table 2 shows the calculation for normalized relative permeability for water saturation (S*w) and the oil and water phases' relative permeability for each curve. Researchers plotted normalized K*ro and K*rw vs. S*w values for all core samples (Fig. 10). Equations 8 and 9 calculated averages for relative permeability to oil at connate water saturation and relative permeability (Table 3). Equations 10 and 11 calculated the average relative permeability to oil and water at connate water and critical oil, respectively (Kro)Swc
and (Krw)Sor. Table 4 represents the final step in this methodology, denormalizing the average curve to reflect the actual reservoir and conditions of Swc and Sro.
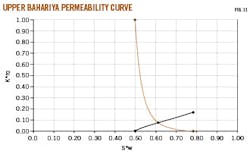
Special core data of the Upper Bahariya reservoir provided an average Swc and Soc of 0.498 and 0.217, respectively. Denormalized relative permeability data generated the reservoir's relative permeability curve (Fig. 11).
Relative permeability curve
The Upper Bahariya's connate water saturation is 48.95%, water saturation at Kro=Krw is 61%, and Krw at maximum water saturation is 17%.5 16
In Fig. 11, Points 1 and 2 represent saturations of residual oil and irreducible water, respectively. Point 3 is the relative permeability to water at residual oil saturation. In a water-wet system the relative permeability at this point ranges from 0.1 to 0.2. Point 4 in Fig. 11 is the relative permeability to oil at the irreducible water saturation. The end points' saturations determine the movable saturation range and are directly related to the amount of recoverable oil. The end points of the relative permeabilities are part of the expression for the mobility ratio and will determine the sweep efficiency of a displacement process.17
Fig. 11 displays the relative permeability functions' curvature. The most prominent feature occurs at the critical saturations where both effective permeabilities drop to 0. Water becomes immobile (Krw = 0) at Sw = Swi (Swi = 48.95%) and oil becomes immobile (Kro = 0) at So = Sor (Sw = 78.3%).
Wettability preference makes Swi larger than Sor. Water ceases to flow at a larger saturation because adhesion binds water to the grain surfaces with a stronger force.
Point 5 on the water relative permeability curve is in the region where most reservoir studies encounter Sw in field displacement. Relative permeability to water is low in this region because oil is trapped in the pores by the invading water.
Capillary pressure
When two immiscible fluid phases, such as oil and water, are present in a porous medium, one of the phases preferentially wets the pore surface over the other. The resulting pressure differential between the two phases is known as capillary pressure. Fluid saturations, interfacial tension between the two fluid phases, and the radius of the pores influence capillary pressure magnitude in a porous medium.4-5 18 Equations 12-13 express capillary pressure for fluid phases in porous media and in terms of the surface and interfacial tension.
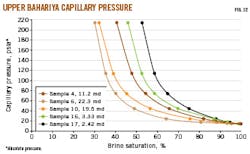
Table 5 presents capillary pressure data for five Upper Bahariya reservoir samples, which reflect how pore geometry effects capillary pressure (Fig. 12). The low-permeability zones have high capillary pressure. The direction of increasing permeability relates to decreasing capillary pressure at certain water saturation.
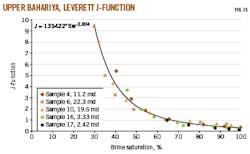
The Leverett J-function is a dimensionless calculation that averages core capillary pressure curves to obtain the most representative curve for a field (Equation 14).6 20-21
Fig. 13 shows the data presented in Table 5. Average permeability and porosity are 11.7 md and 17.4%, respectively. The best-fit line in Fig. 13 shows the best-fitted J-function (Table 6). This methodology can calculate the capillary pressure from Table 6 with average porosity and permeability values (Equation 15).
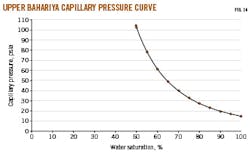
The values in Table 7 can approximate these results in the absence of laboratory data.20 The laboratory fluid system did not match the surface tension of the reservoir system, suggesting the study's core sample may not have represented the reservoir's average permeability and porosity. Equation 16 converts laboratory capillary pressure to reservoir capillary pressure (Table 7). Fig. 14 shows the resulting capillary pressure curve.
Upper Bahariya curve
Lithology, high connate water saturation, and high heterogeneity causes Upper Bahariya's capillary pressure curve to resemble a transition zone. Displacement requires increasing oil pressure until the pores with the smallest capillary pressure give way, making the oil-water pressure difference greater than the required capillary pressure. Intuitively, these would be the largest pores.
Displacement pressure is the minimum capillary pressure required for invading the rock and reducing water saturation below 100%. Fig. 14 indicates a 15 psia displacement pressure for Upper Bahariya.
Displacement pressure increases steadily with decreases in water saturation as smaller pores are invaded. The slope of the capillary pressure curve follows the gradual change in pore diameters, and a steep curve indicates a wide distribution.
Displacement pressure can also indicate the wettability preference of the rock. A positive displacement pressure in an oil-displacing-water process indicates preferential wettability to water and the relative magnitude of the displacement pressure reflects the strength of such wettability.References
1. Shedid, S.A., and Almehaideb, R.A., "Robust Reservoir Characterization of UAE Heterogeneous Carbonate Reservoirs," SPE No. 81580, Society of Petroleum Engineers (SPE) 13th Middle East Oil Show and Conference, Bahrain, Apr. 5-8, 2003.
2. Jensen, J.L., and Currie, L.D., "A new Method for Estimating the Dykstra-Parsons Coefficient to Characterize Reservoir Heterogeneity," SPE Reservoir Engineering, Vol. 5, No. 3, August 1990.
3 Alharbi, A.M., "Experimental Evaluation of the Effect of Carbonate Heterogeneity on Oil Recovery to Water and Gas Injection," PhD thesis, University of Calgary, September 2013, pp. 11-12.
4. Ahmed, T., "Reservoir Engineering Handbook," 2nd Ed., Gulf Publishing Co., Houston, 2002.
5. Satter, A., Iqbal, G.M., and Buchwatter, J.L., "Practical Enhanced Reservoir Engineering Assisted with Simulation Software," PennWell Corp., Tulsa, 2008.
6. Tiab, D., and Donaldson, E.C., "Petrophysics: Theory and Practice of Measuring Reservoir Rock and Fluid Transport Second Edition," Gulf Publishing Co., Houston, 2004.
7. Fitch, P., Davies, S., Lovell, M., and Pritchard, T., "The Petrophysical Link between Reservoir Quality and Heterogeneity: Application of the Lorenz Coefficient" Society of Petrophysicists and Well-Log Analysts (SPWLA), No. SPWLA-2013-Q, SPWLA 54th Annual Logging Symposium, New Orleans, June 22-26, 2013.
8. Lake, L.W., and Jensen, J.L., "Review of Heterogeneity Measures Used in Reservoir Characterization" SPE No. 20156-MS, Jan. 1, 1989.
9. Archer, J.S., and Wall, C.G., "Petroleum Engineering: Principles and Practice" Graham & Trotman Ltd., London, 1986.
10. Abbaszadeh, M., Fuji, H., and Fujimoto, F., "Permeability Prediction by Hydraulic Flow Units Theory and Application," No. SPE-30158, SPE PetroVietnam Conference, Ho Chi Minh, Mar. 1-3, 1996.
11. Deghirmandjian, O., "Identification and Characterization of Hydraulic Flow Units in The San Juan Formation, Orocual field, Venezuela" MS thesis, Texas A & M University, May 2001.
12. Al-Ajmi, F.A., and Holditch, S.A., "Permeability Estimation Using Hydraulic Flow Units in a Central Arabia Reservoir," No. SPE-63254, SPE Annual Technical Conference and Exhibition, Dallas, Oct. 1-4, 2000.
13. Ali, S.S., Hossain, M.E., and Abdulraheem, A., "Hydraulic Unit Estimation from Predicted Permeability and Porosity Using Artificial Intelligence Techniques," No. SPE-164747, North Africa Technical Conference and Exhibition, Cairo, Apr., 15-17, 2013.
14. Nejad, T., Borhani, G., and Emadi, S.H., "Application of Hydraulic Flow Units and Intelligent Systems for Permeability Prediction in a Carbonate Reservoir," Curtin University Technology, Science, Engineering International Conference, Miri, Sarawak, Malaysia, Nov. 8-9, 2011.
15. Desouky, S.E., "Predicting Permeability in Un-Cored Intervals/Wells Using Hydraulic Flow Unit Approach," Journal of Canadian Petroleum Technology, Vol. 44, No. 7, July 2005.
16. Craig, Jr., F.F., "Reservoir-Engineering Aspects of Waterflooding Second Printing," American Institute of Mining, Metallurgical, and Petroleum Engineers Inc., Dallas, 1971.
17. Torsaeter, O., and Abtahi, M., "Experimental Reservoir Engineering Laboratory Work Book," Department of Petroleum Engineering and Applied Geophysics, Norwegian University of Science and Technology, August 2000.
18. Sivila, L.J., "A Petrophysical Evaluation of Capillary Pressure for Naturally Fractured Tight Gas Sandstone (Reservoir: A Case Study)," MS thesis, Colorado School of Mines, 2004.
19. Abu-Khamsin, S.A., "Basic Properties of Reservoir Rocks," King Fahd University of Petroleum and Minerals, 2004.
20. Timmerman E.H., "Practical Reservoir Engineering Part-1" PennWell Publishing Co., Tulsa, 1982.
The authors
Abdel Wahab Bayoumi ([email protected]) is professor of petroleum engineering at Al-Azhar University, Cairo. He served the Petroleum and Mining Engineering Department as chairman from 2007 to 2012. He also has served as a natural gas production engineer at Gulf of Suez Petroleum Co. and the Egyptian General Petroleum Corp. from 1981 to 1984. He holds a BS and MS in petroleum engineering from Al-Azhar University and a PhD in petroleum engineering from the Oil and Gas Institute, Ploiest, Romania. He is a member of the Egyptian Engineers Syndicate and SPE.
Sayed Gomaa ([email protected]) is an associate professor of petroleum reservoir engineering at Al-Azhar University and the British University in Egypt. He holds a BS and MS in petroleum engineering from Al-Azhar University and a PhD in petroleum engineering from Azerbaijan State Oil Academy, Baku.
Abdelnaser Hamdy ([email protected]) serves as head of the petroleum engineering department at Khalda Petroleum Co. Prior to this, he served as head of Khalda's reservoir management engineering team. He holds a BS in petroleum engineering from Al-Azhar University and is currently finalizing his MS. He is a member of the Egyptian Engineers Syndicate and SPE.