Interface calculation method improves multiproduct transport

At instant t0 Fluid B covers the entire volume of the pipe and the two fluids are in perpendicular contact relative to the pipeline axis (x = 0). During subsequent flow at the instant t1 an interface forms in the contact zone and the concentration of fluid B varies from CB = 1 at the beginning of the mixing zone to CB = 0 at the end of that area (x = x1). Fluid A, meanwhile, varies from CA = 0 to CA = 1.

Interface length between Fluids A and B evolves further over time (x = x2). But diffusion helps separate the fluids in the mixing zone, creating an area where the concentrations are assumed equal (CA = CB = 0.5). The interface is generally characterized by the mixture concentration curve variation.^1-3

Mass transfer in the two fluids' contact area conditions the mixture. Mass transfer tends to be determined by the convection mechanism in the base flow (center of the pipe) and the molecular diffusion mechanism near the walls. Given the high flow rates usually present in a pipeline, molecular diffusion's contribution is negligible.⁴

Experimental study

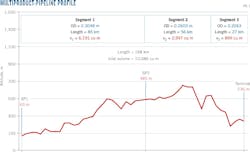
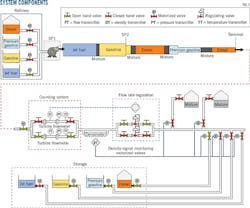
A 168-km multiproduct pipeline linking a refinery in western Algeria to storage and fuel distribution centers served as the experiment site. The pipeline has three segments of different diameters and lengths (Fig. 1). Table 1 summarizes the transported fuels' densities. Other system components (Fig. 2) include:

• A refined-products tank farm at the refinery.

• Two pumping stations.

• A receiving center including fuel storage.

Fuels moved in batches from the refinery tank farm through SP1 pump station. A vertical contact was established between batches as each was introduced, with the subsequent mixing zone developing and progressing until reaching the terminal at pipeline's end. The number of mixing zones depends on the number of batches introduced to the pipeline.

A counting system and electronic densimeter installed at the end of the pipeline dispatch products to the appropriate tank by direct measurement of density. Density ranges were entered in the pipeline's distributed control system (DCS) before shipment.

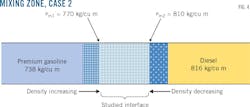
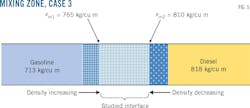
Pure fuels go to storage tanks and mixtures to their destination tanks. Mixture volume is recorded by a certified measuring gauge, by the direct reading of levels (initial and final height of tank), and displayed by the supervisory system. The mixtures had densities of 770-810 kg/cu m and 765-810 kg/cu m.

Mathematical model

The flow of particles in a given direction can have two origins: one is the concentration gradient, the other the action of a transporting force which causes the particles to move with a certain mean velocity.⁵ According to the continuity equation and Fick's law, the mathematical model describing the convection-diffusion process is shown in Equation 1.⁶

With Fluid B followed by Fluid A, Equations 2-7 describe the beginning of sequential flow in terms of CB.^{7 8} The mixing intensity in the longitudinal direction can be expressed by the diffusion coefficient, D, which correlates the physical properties of the medium and the flow system. We selected eight empirical correlations from different investigations of petroleum products (Equations 8-15).^{4 9}

Viscosity measurement of Fluids A and B is based on the Gambill correlation10 expressed by Equations 16-18. Solutions for convection-diffusion equations are similar as those for pure diffusion equations, except for replacing X by x - ut, represented by Equation 19.

Observing the flow of Fluids A and B in the pipeline at a constant rate with variation in the diameter exposes the mixture's evolution along the pipe. Equations 20-22 are the mathematical expression of this evolution. Equation 23 expresses the extreme end-of-pipe case, x = L. Since fluids flow with constant average velocity in each section of pipe, substituting xn and L in the equation of X yields Equations 24-25.

Substituting the value of x in the Z cut-off concentration argument (Equation 19) yields Equation 26. In the final section of the pipe, t tends toward t0 and thereafter θ = 1, leading first to Equation 27 and then Equation 28. Equations 29 and 30 provide the mixture volume, Vm, which passes through the cross section of the pipe at a given time (t1, t2).^{4 11} These in turn yield Equations 31-33.

Diffusion coefficient D also depends on the pipe geometry and Reynolds number, leading to Equation 34. Accounting for the constancy of the average velocity in the same section and consequent Reynolds number yields Equation 35.

The mixing zone can be subdivided into three parts, differentiated by two cut-off concentrations, CB1 and CB2. These two parts represent the beginning and the end of the mixing zone and can be respectively added to Liquids A and B without altering their physicochemical characteristics. The intermediate area is the real mixture volume that will be predicted theoretically and evaluated experimentally because its injection in unstudied quantities into one of the two fuels may immediately affect their quality.

The cut-off concentrations will determine arguments Z1 and Z2 and formula ∑ mi = m (i = A, B)12 yields the admissible concentrations in the mixture shown in Equations 36-37.

Results

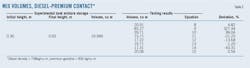
The two interface types used were diesel-premium gasoline and gasoline-diesel. Tables 2-4 show the theoretically calculated and experimentally recorded mixing volumes. Conversion to percent deviation (%D) used Equation 38.13 The percent deviation allows selection of correlations providing good approximation and an acceptable relative error.

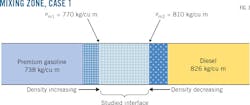
Fig. 3 shows the first case of diesel-premium gasoline contact, with the evolution of densities up to the mixing zone bounded by the densities ρm1 and ρm2. Tank-level measurement showed 19.949 cu m as the mixture volume for diesel-premium gasoline contact, with 826 kg/cu m and 738 kg/cu m the respective densities of diesel and premium gasoline, a flow rate of 180 cu m/hr, and a mean temperature of 20.5 °C. (Table 2).

The second case used the same contact but different densities than those from the first case (Fig. 4). Density limits were the same. The mixture volume was 26.172 cu m, with 816 kg/cu m and 738 kg/cu m the respective densities of diesel and premium gasoline, a flow rate of 176 cu m/hr, and a mean temperature of 20.3 °C. (Table 3).

Fig. 5 shows a gasoline-diesel interface where the mixing area is also bounded by the densities ρm1 and ρm2 but with ρm1 taking the gasoline-dependent value. Table 4 shows a mixture volume of 28.998 cu m as this contact's volume, with 713 kg/cu m and 818 kg/cu m as respective densities of gasoline and diesel, a flow rate of 176 cu m/hr, and a mean temperature of 26.1 °C.

The correlations represented by Equations 8, 13, and 15 approximate the experimental field results. Equation 15, however, is the most accurate (-1.92<%D<0.91) and can be best used to reduce interface length and minimize the mixing zone during multiproduct transport. Failure to do so would require building large-volume storage parks for segregation of mixed volumes.

References

1. Zheng, C.M., and Bennett, G.D., "Applied Contaminant Transport Modeling: Theory and practice," John Wiley & Sons, Hoboken, NJ, 1997.

2. Baptista, R.M., Freitas Rachid, F.B., and Carneiro de Araujo, J.H., "Mixing Volume Evaluation under Pumping Shut-Down Conditions," Pipeline Simulation Interest Group Conference, Salt Lake City, Oct. 17-19, 2001.

3. Oliveira, J. L., "Modeling the dispersion phenomenon in batch transfer operations by the theory of structured mixture," Brazilian Journal of Petroleum and Gas, Vol. 4, No. 4, pp. 129-138, October-December 2010.

4. Demoya, A.C., Cruz, H.Q., and Benjumea Hernandez, P.N., "Modelling of the Pollutant Fronts Generated by Pipeline Fuel Transportation," Dyna, Vol. 74, No. 152, pp. 89-96, January 2007.

5. Crank, J., "The Mathematics of diffusion," 2nd Ed., Clarendon Press, Oxford, 1975.

6. Brannan, J., Cumberbatch, E., Moodie, B., Myers, T., O'Connell, G., and Pickering, D, "Density Driven Turbulent Mixing at Batch Interfaces," Pacific Institute for the Mathematical Sciences Industrial Problem Solving Workshop, University of Victoria, May 31-June 4, 1999.

7. Baptista, R.M., Freitas Rachid, F. B., and Araújo J.H.C., "Predicting Mixing Volumes in Serial Transport in Pipelines," Journal of Fluids Engineering, Vo. 124, No. 2, pp. 528-534, June 2002.

8. Baptista, R. M., Freitas Rachid, F. B., and Araújo J.H.C., "The influence of pipeline diameter variation on the mixing volume in batch transfers," International Pipeline Conference, Calgary, Sept. 29-Oct. 3, 2002.

9. Aunicky, Z., "The longitudinal mixing of liquids flowing successively in pipelines," The Canadian Journal of Chemical Engineering, Vol. 48, No. 1, pp. 12-16, February 1970.

10. Vanaparthy, S.H., and Meiburg, E., "Variable density and viscosity, miscible displacements in capillary tubes," European Journal of Mechanics-B/Fluids, Vol. 27, No. 3, pp. 268-289, May-June 2008.

11. Abart, R., and Petrishcheva, E., "Mathematics of Diffusion Problems," Free University Berlin, Apr. 19, 2006.

12. "Flow of Fluids through Valves, Fittings and Pipe," Technical Paper No. 410M, 21st Ed., Crane Co., 300 Park Ave., New York, NY.

13. Patrachari, A.R., "Deterministic model to explain the phenomenon of interfacial mixing in refined products pipelines," Oklahoma State University, Dec. 1, 2012, p. 106.

The authors
Djamel Bennacer ([email protected]) is terminal manager of a multiproduct pipeline for Sonatrach subsidiary Naftal SPA and a PhD student in mechanical engineering at University of Tlemcen, Algeria. He has also served as technical supervisor of multiproduct pipeline and tank construction for Naftal, and industrial mechanical supervisor at Sonatrach's Arzew LNG complex. He holds an engineer degree (2000) and a magister degree (2011) in mechanical engineering from University of Tlemcen. He is member of the energetic and applied thermal laboratory (ETAP) at University of Tlemcen.
Rachid Saim ([email protected]) is a professor of mechanical engineering at University of Tlemcen. He received his PhD (2008) in energetic mechanics at Tlemcen University. His research focuses on convection in complex geometry applied to thermo-solar converters and heat exchangers. He is also a researcher at ETAP and is chief of the solar thermal conversion team.
Said Abboudi ([email protected]) is a professor at the University of Technology of Belfort-Montbéliard (UTBM), Belfort, France He received his first PhD (1982) and his second PhD (1988) in heat transfer applied to the solar system at Aix-Marseille University 1, Marseille, France. His domain of research concerns heat and mass transfer (conduction, convection), thermo-physical coupling, inverse problems, and applications to thermal systems.
Benamar Benameur ([email protected]) is a PhD student in mechanical engineering at University of Tlemcen, Algeria. He served as a research assistant (2013-14) at the scientific research unit of renewable energies (URER-MS/CDER), Adrar, Algeria. He holds an engineer degree (2009) and magister degree (2012) in mechanical engineering from University of Tlemcen. He is a member of ETAP.