New method evaluates efficiency of wellbore stimulation operations
I.M. Kutasov
Pajarito Enterprises
Santa Fe, NM
L.V. Eppelbaum
Tel Aviv University
Tel Aviv
A new technique has been developed for analyzing the bottomhole pressure at constant flow rate drawdown well tests. The method presented in this article enables calculation of the skin factor for stimulated oil wells.
Only records of the flowing time and bottomhole flowing pressure data are required to compute the value of the skin factor.
A semitheoretical equation was earlier suggested to approximate the dimensionless bottomhole pressure. This formula is used to obtain a quadratic equation for determining the skin factor. The suggested method can be utilized by production managers to evaluate the efficiency of wellbore stimulation operations. The article includes an example of calculation.
Introduction
As a consequence of drilling and completion operations, most wells have reduced permeability near the borehole (skin zone).
At oil-water production the radius of the skin zone increases over time. It is known that reservoir waters associated with oil-bearing formations contain a variety of dissolved solids (scales). At simultaneous production of oil and water, precipitation of scales occurs.
In the vicinity of the well the pressure logarithmically increases with the radius. As a result deposition of scales mainly occurs near the wellbore. Due to partial blocking of pores a skin is created whose size increases with production time.
A comprehensive study of the essential mechanisms of formation damage by pore blocking can be found in the literature.1
Deposition of scales in the pores greatly reduces the permeability of formations around the wellbore. This results in pressure loss through the skin and a corresponding reduction in well productivity. Well stimulation through acidizing or hydraulic fracturing can improve well productivity even above production levels in undamaged conditions. Quantitatively, the skin is defined as a parameter (skin factor), which depends on the thickness and the effective permeability of the skin zone2 (Equation 1).
It is more convenient to express the skin factor through the apparent (effective) well radius3 (Equation 2).
The main fracture parameter, fracture length (L), is defined as L = 2rwa.
A well with a negative value of the skin requires a much smaller pressure drop in comparison with a well with a positive skin factor to maintain a constant fluid flow rate (Table 1, columns 5 and 6). For hydraulically fractured wells, the rwa/rw ratio can be very large.
We will assume that for stimulated wells (s < 0) the apparent radius concept can be used. In practice this means that the drainage radius4 should be considerably larger than the apparent radius.
This article describes a new method for determining the skin factor that enables evaluation of the efficiency of wellbore stimulation operations (hydraulic fracturing or acidizing). For this reason we assume that the formation permeability was estimated from previous buildup or drawdown pressure well tests.
A well as a cylindrical source
For stimulated wells the value of dimensionless time based on the apparent radius (Equation 2) can be small and the wellbore should be considered to be a cylindrical source.
Let's assume that a well is producing at a constant flow rate from an infinite-acting reservoir with the following characteristics: the reservoir is a homogeneous and isotropic porous medium of uniform thickness, the porosity and permeability are constant, the fluid is small and has constant compressibility, constant fluid viscosity, small pressure gradients, negligible gravity forces, and laminar flow in the reservoir and the Darcy law can be applied.
For a well as a cylindrical source we need to obtain the solution to the diffusivity equation under the boundary and initial conditions in Equations 3 and 4.
It should be noted that conventionally in reservoir engineering the produced flow rate q (Equation 3) has a positive sign, and a negative sign is applied to injection wells. It is well known that in this case, the solution to the diffusivity equation is a complex integral.5 6
For the bottomhole pressure (in terms of pressure and fluid flow rate) we obtained the semianalytical Equations 5 and 6.7
Let's introduce the dimensionless wall pressure as Equation 7. Then see Equation 8.
Values of pD calculated from Equation 13 and the results of a numerical solution ("Exact" solution) by Chatas8 were compared.7 The agreement between values of pD calculated by these two methods was very good. For this reason the principle of superposition can be used without any caveats.
Equation 8 can be rewritten as Equation 9.
See Equation 10, then see Equation 11.
The solution of Equation 11 is Equation 12.
The apparent (effective) well radius skin factor is calculated from Equations 2 and 6 (see Equation 13).
This yields a quadratic equation for estimating the skin factor. It is interesting to note that we obtained a similar equation for the calculation of the skin factor for a well produced at a constant bottomhole pressure.9
Example
It is routinely accepted that the first step in validation of a suggested new method is to use an "Exact" (numerical) solution and generate data for a simulated test.
Subsequently a semianalytical equation is used to process the results of the simulated test and compare the obtained and assumed input parameters. Below we used the results of a field drawdown well test from Earlougher, 1977, Example 3.1.3
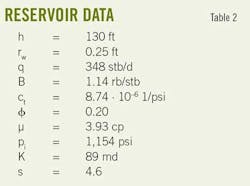
The reservoir and test data are presented in Table 2. It was found that the deviation from Horner plot caused by the skin and borehole storage effects was observed during the first 4 hr. The duration of the transient period was 12 hr, and at t > 16 hr the pressure behavior was influenced by reservoir boundaries, interference from nearby wells, neighboring boundaries, interference from nearby wells, and-or other factors. Let's now assume that after well stimulation the skin factor was lowered from s = 4.6 to s = –5.108.
Using the Table C.1 in Lee8 of pD = f(tDa), we generated data for this simulated example (Table 2). The value of s = –5.108 was selected to avoid interpolation of pD values. This yielded Equation 14.
The results of Equations, 6, 12, and 13 are presented in Table 1. The calculations show that Equation 5 can be used to compute the flow pressure and skin factor. The assumed and calculated values of the skin factor are in very good agreement.
A new method for analyzing the constant flow rate pressure test data has been presented. This method can be used to calculate the skin factor for stimulated wells. It can be applied by oilfield service companies to evaluate the efficiency of wellbore stimulation operations (hydraulic fracturing or acidizing). To verify the applicability of the suggested method, field experiments in boreholes are needed.
References
1. Schechter, R.S., "Oil Well Stimulation," Prentice Hall, Englewood Cliffs, NJ, 1992.
2. Hawkins, M.F. Jr., "A note on the skin effect," Trans. AIME, Vol. 207, 1956, pp. 356-57.
3. Earlougher, R.C. Jr., "Advances in Well Test Analysis," SPE, 1977.
4. Eppelbaum, L.V., and Kutasov, I.M., "Pressure and temperature drawdown well testing: similarities and differences. Journal of Geophysics and Engineering, Vol. 3, 2006, pp. 12-20.
5. Van Everdingen, A.F., and Hurst, W., "The Application of the Laplace Transformation to Flow Problems in Reservoirs," Trans. AIME, Vol. 186, 1949, pp. 305-24.
6. Carslaw, H.S., and Jaeger, J.C., "Conduction of Heat in Solids," 2nd Edition, Oxford Univ. Press, UK, 1959.
7. Kutasov, I.M., "Dimensionless temperature at the wall of an infinite long cylindrical source with a constant heat flow rate," Geothermics, Vol. 32, 2003, pp. 63-68.
8. Lee, J., "Well Testing, SPE Monograph Series, 1982.
9. Kutasov, I.M., and Kagan, M., "Determination of the Skin Factor for a Well Produced at a Constant Bottomhole Pressure," Journal of Energy Resources Techn., Vol. 125, March 2003, pp. 61-63.