ASSET INTEGRITY-1: New model predicts internal corrosion likelihood
Fengmei Song
John McFarland
Barron Bichon
Southwest Research Institute
San Antonio
Luc Huyse
Chevron USA Inc
Houston
Fraser King
Integrity Corrosion Consulting, Ltd.
Nanaimo, BC
Laurie Perry
Southern California Gas Co.
Los Angeles
Mark Piazza
Pipeline Research Council International
Falls Church, Va.
Defining the term "extremely unlikely internal corrosion threat" to be 20% wall loss within 50 years allowed development of a probabilistic model for predicting whether an IC threat, under a nominal operating condition, is extremely unlikely.
With a confident determination of the conditions in which an IC threat is extremely unlikely, operators may be able to present a case to regulators to extend the reassessment interval of in-line inspection, pressure tests, or direct assessment for IC.
The model followed a comprehensive statistical analysis of field data collected from operators, including operating temperature, pressure, and water content. Operating gas temperature tends to follow a sinusoidal relation with the season, while pressure is relatively stable over time. Actual water content (wc) in gas tends to be much lower than 7 lb/MMscf, the typical threshold limit. A conservative lognormal distribution of WC was developed and used in the modeling.
The first article of this series, presented here, defines the objective of the process underlying this series, model inputs, and field conditions. The conclusion (OGJ, Feb. 7, 2011) will detail the probabilistic model and computational results.
Background
The US Pipeline Safety Regulations, Code of Federal Regulation (CFR) 192.921(a) requires pipeline integrity assessments be conducted by in-line inspection, pressure testing, direct assessment, or some other technology through which the operator demonstrates an equivalent understanding of the condition of the pipeline.1
Each of the methods has limitations. In-line inspection cannot be performed on pipelines that lack launchers or receivers, have narrow-radius fittings or valve obstructions or multidiameter pipes or for which service interruptions become impossible because of cost or critical customer impact.
Pressure testing is not useful for detecting subcritical defects that might grow at a high velocity. If conducted with water, such testing could also bring in corrodants including the water itself, salts, and bacteria. Pressure testing typically involves the most costly service interruptions and provides the least descriptive data for future planning. Internal corrosion direct assessment2-4 applies only to small portions of a pipeline segment because the cost associated with excavation is enormous. Road and water obstructions can also inhibit direct assessment.
Selecting a baseline assessment method requires identifying all threats to a pipeline. This article, however, will limit itself to evaluating the IC threat. The limitations of pipeline integrity-assessment methods make the ability to determine and prioritize the most likely locations of IC threat important.
Prioritization of IC-susceptible locations becomes especially important for IC direct assessment because only a small fraction of the pipe will be directly examined requires inspection be performed where the probability of IC is greatest. Confidence associated with the prioritization allows only locations with the highest priority of IC threat be selected for excavation. Other locations need not be considered except for validation purposes.
The extent of water content (WC) in natural gas pipelines directly affects prioritization of excavation locations. For wet gas pipelines,3 water may be present everywhere on the pipe's internal surface and thus the basis for the prioritization is the severity of corrosion. By contrast, for dry gas (DG) pipelines,4 gas quality control requires WC not exceed certain threshold limits (TL),4 making the likelihood of IC in these pipelines low. The main element determining location of an IC threat is where liquid water occurs due to water condensation, liquid water intrusion from laterals, or leftover hydrotest water.
This article focuses on DG pipelines only.
DG pipelines are transmission or distribution pipelines that carry nominally DG.4 Normally DG is natural gas with WC controlled under nominal 7 lb/MMcf or in cold regions, 5 lb/MMcf.4 Precise definition of DG and the units of WC will occur in a later section.
Absence of liquid water at the pipe's internal surface removes the medium required for electrochemical reactions, making corrosion impossible. The probability of water condensation in DG pipelines can be low, but it can occur when water dewpoint rises above operating temperature. Variation in gas quality between suppliers and sometimes for the same supplier makes water condensation possible: gas quality varies with sources of gas. Operating conditions (temperature, pressure, flow rate, and WC) of the pipelines also vary with time and location along the pipeline.
Water condensation, liquid water leftover from earlier hydrotests, periodic intrusion of liquid water, or injection of wet (or saturated) gas from side laterals can also lead to an IC threat. The presence of solid salts, corrosion products, or biofilms on the pipe's internal surface; the presence of inhibitors; the intrusion of compressor oil; and the leaking of dehydrates from upstream dehydration units can all affect IC. Difficulty in quantifying the roles of these factors, including condensation and direct liquid water intrusion in the IC of DG pipelines, makes confident determination of the most likely IC locations, let alone determining the most severe IC locations, problematic.
Determining with certainty locations having an extremely unlikely IC threat can save costs by eliminating these locations from further evaluation for IC. This concept is as important as determining the most likely locations for IC threat. This concept is particularly important for DG pipelines because, if operated properly, it is possible that the vast majority of such pipeline sections can be eliminated from consideration of an IC threat.
Even though water can lead to IC, corrosion severity may not be of concern in many instances, for instance if the liquid water is present for a very short duration or the corrosion rate is extremely low. When only one hydrotest is performed for a DG line within 50 years of its operation, for example, if the hydrotest water was properly cleaned and dried out immediately following the test, the overall duration of water presence in the line can be short and the accumulated wall loss due to the leftover hydrotest water can be insignificant.
A pipeline section with known extremely infrequent liquid water intrusions could likewise suffer corrosion, but very short duration of liquid water's presence would make the IC threat extremely low. Even with frequent upsets or liquid water intrusion, the implementation of effective inhibition can reduce the threat it poses. It is also possible for the liquid water to evaporate rapidly in the carrying DG.
Even though IC threat in DG pipelines is generally low, the threat does exist. US regulation CFR 192.9391 requires the reassessment interval for inspections be set not to exceed 7 years. Even when a reassessment interval is allowed to be greater than 7 years, the operator must, within the 7-year period, conduct a confirmatory direct assessment on the covered segment, and then conduct a follow-up reassessment at the interval the operator has established.
The cost associated with in-line inspection, pressure testing, or direct assessments relative to the generally very low IC threat (perhaps for a large portion of the DG pipeline) may make the 7-year reassessment interval seem excessive for IC threat. But this position cannot be effectively justified without particular evidence in a particular instance showing the interval to be too short.
Objective
The project underlying this article sought development of an approach to determine pipeline operating conditions with an extremely low likelihood of IC, focusing on water condensation as the corrosion cause. Determining these conditions could exempt lines from expensive in-line inspection, pressure testing, or direct assessment, extend the reinspection or reassessment interval, or at minimum reduce the portion selected for inspection or validation to as small as possible.
This approach requires the concept of "extremely unlikely IC threat" be quantitatively defined, for example, below what level of WC an IC threat can be considered extremely unlikely. Determining the upper boundary of WC, allows its use in assessing whether the current TL of 7 or 5 lb/MMcf is suitable, that is, whether the industry's current nominal operation of DG pipelines, with the WC controlled under such a TL, falls within the conditions of extremely unlikely IC threat.
The operating condition of a specific pipeline allows prediction of its remaining life from the model. This predicted remaining life can then help assess if the 7-year reassessment interval is excessive, what interval is more appropriate, or how operating conditions need to be adjusted to reach desired remaining life.
The overall scope of the work covered the following three cases of IC threat for DG pipelines based on sources of liquid water:
- Possible water condensation.
- Gas quality upsets, liquid water intrusion from laterals.
- Hydrotest water leftover.
Limited by space, this article covers only the first case, possible water condensation. Since the model deals with likelihood of IC threat, it is probabilistic in nature.
Developing the probabilistic model requires quantitatively defining the term extremely unlikely corrosion threat, understanding the concept of DG and TL, predicting the saturation limit (SL) of a gas, and knowing the characteristics of nominal pipeline operating conditions. These comprise the model input parameters.
Model inputs
No quantitative definition exists in the literature for the term "an extremely unlikely corrosion threat." The lower the IC threat, however, the smaller is the wall loss within a defined life time. Several operators agreed that as long as pipe wall loss can be controlled with confidence not to exceed 20% WT within 50 years, the IC threat of this condition may be considered extremely unlikely.
DG is nominally defined as gas with WC falling under a TL with typical humidity <7 lb/MMscf in the US except in its northern region, which shares at 5 lb/MMscf threshold with Canada. (MMscf is a million standard cubic feet, standard defined by IGT-85 as 1 atm and 15° C. or 59° F.)
Equation 1 converts English WC units into metric units, yielding normal TL for water of 5 lb/MMscf = 80.1 mg/standard cu m, and 7 lb/MMscf = 112.1 mg/standard cu m.
The unit of WC represents a mole fraction. Ideal gas law holds for the standard condition with a low pressure and low temperature (1 atm and 59° F., Equation 2)
This law allows conversion of lb/MMscf as shown in Equation 3, yielding mole fractions of 7 lb/MMscf = 1.473 × 10-4, and 5 lb/MMscf = 1.052 × 10-4.
Understanding TLs or gas quality for nominal corrosive constituents, including WC and contents of CO2 and H2S, provides an understanding of the upper bounds of these constituents and their respective corrosivity.
When IC occurs, the partial pressure of CO2 plays a key role in determining corrosion rate. Although H2S in gas and the presence of solid sulfur can result in corrosion, perhaps neither is as significant as CO2. H2S in low concentrations was actually found to mitigate CO2 corrosion.6 Oxygen (O2) can result in a high rate of IC but is not commonly present in pipelines. Oxygen's presences requires considering the corrosion rate resulting from it.
The importance of understanding the contents of the corrosive constituents in gas justifies a brief review of an earlier study conducted in 1999 by the Gas Machinery Research Council and Southwest Research Institute.7 The 1999 study sought to understand at what content the gas was regulated to be controlled under for a particular corrosive constituent or TL. For this study, the terms of agreement for 70 companies were collected and collated to identify how the gas threshold limits were dealt with given the minor quantity of corrosive components in natural gas in the US.
Fig. 1 plots the original survey data.7 The value shown on each segment of a column is the TL for that specific corrosive constituent, labeled at the bottom of the column including the TL unit. Of the 70 companies surveyed, the number that responded to follow a TL is shown on the left vertical and the percent on the right.
Fig. 1 shows the TL for WC at 7 lb/MMscf to be most widely accepted. Other WC are lower and more applicable to colder climates where water dewpoint is lower. The two predominant TLs for CO2 content are 2% and 3% by volume. Using nitrogen as an inert element moves the TL's combined limit to 3%, or CO2 alone to 2%.
Many companies thought O2 to be nonexistent in gas pipelines, as noted by the rather large number of companies missing a standard for it. A 0.20% nitrogen content appears to be the majority limit.
The most common standard for H2S content is one-quarter grain/100 cu ft gas, or 4 ppm. Close to half the TLs support this value while the ones deviating from it are all on the high side. An H2S content of 16 ppm also appears to be widely accepted.
For total sulfur in all forms, over half the industry recognizes 20 grains/100 cu ft gas as an upper limit. Over one-third more are below this level, 5 grains being the second most popular threshold.
The probabilistic modeling uses the TLs for water and CO2. The water threshold limit helps develop the operating charts, while the CO2 TL is used for determining the corrosion rate when the de Waard-Lotz equation is being used.8
The standard methods used by the gas industry for determining water saturation limit (SL) or dewpoint include AGA Monograph 8, IGT-8/ASTM D1142, GPA Engineering Data Book, and the GERGWATER method. The third-order Peng-Robinson equation of state (EOS) can also serve this purpose.9 Comparing the different methods showed the IGT-8 method offering predictions between those of the other methods, suggesting its predictions are modest relative to the others. IGT-8 determines water SL in this article (Equation 4).
The values of A and B are tabulated in the IGT-8 manual5 and yield Equations 5 and 6 if fitted by polynomial expressions.
Fig. 2 shows the fit of Equations 5 and 6 to the tabulated data given by IGT-8 to be excellent. The fitting curves pass through the center of each data point within the conditions shown in the figure, which cover the limits of normal pipeline operations well.
Field conditions
Developing a probabilistic model for field application requires understanding actual distributions of the operating parameters. Operators collected field data of pipeline operating temperature, pressure, and water content at different locations along their systems. Comprehensive statistical analysis of the data sought to understand variability with time of the operating temperature, pressure, and WC, assumed sufficiently to represent variability of the operating conditions across the industry within the US and Canada.
The statistical results of temperature and pressure can determine the distribution of dewpoints with Equation 4. The probability of water content exceeding dewpoint is the probability of water condensation, a basis used for developing the probabilistic model.
The project collected field time-dependent temperature and pressure data for a total of 38 independent lines from six operators across the US and Canada, gathering at least 1 year of data for each set so seasonal variation could be clearly seen.
Fig. 3 shows the typical variation of gas temperature and pressure vs. time for one point of a line during less than 3 years of operation. Pressure appears to be relatively stable over time, fluctuating roughly around its average. Temperature varies periodically with the seasons, higher in summer and lower in winter. Periodic variation of the ground temperature may lead to this variation (Fig. 4), though the exact reason is not totally clear. Fig. 4 shows data recorded in Edmonton, Alta., of air and soil at a normal pipeline depth without the actual presence of a pipe.10
Analysis of field temperature data vs. time reveals that temperature can generally be expressed by a sinusoidal expression (Equation 7).
Data shown in Fig. 5 (same data as Fig. 3) can be well fit by Equation 7, where the yearly average temperature, μT, = 87.60° F. and the average amplitude of seasonal temperature variation, AT, = 16.01° F. The unit of time, t, is days, the frequency of seasonal temperature variation, ω, = 2π/365.25, and the phase in the sinusoidal function in Equation 7, θ, = 4.11. The start time determines θ. Fig. 5 also shows the residual fit.
Analyses of all data sets of temperature uncovered three categories. In Category 1, to which a majority of the field data belong (25 of the 38 lines), temperature follows a sinusoidal relation with time due to seasonal change and pressure can be estimated by its average. Fig. 3 is a typical figure of this category.
In Category 2 field data appear to consist of two different sinusoids (Fig. 6). Two distinct upper-lower operating conditions are shown, respectively, for (a) temperature and (b) pressure. Both can be separated out and one sinusoidal model can fit both sets of temperatures. Although the pressure fluctuates, the overall average can still be used to represent the data because it is less sensitive to dewpoint than temperature.
Category 3 contains field data following no clear trend. Fig. 7 shows a large variation in temperature.
Fig. 8(a) shows the temperature seasonal variation vs. temperature average for the 28 lines whose time-dependent temperature can be expressed by a sinusoidal expression. Fig. 8(b) and (c) show, respectively, distributions of temperature mean and amplitude data. In Fig. 8(b) with temperature varying between 39-120° F., the mean temperature is 70.2° F., falling in the category 60-80° F. which has more data points than any other. For temperature amplitude, Fig. 8(c) shows a range of 5-22° F., a mean of 10.8° F. and most data points falling in the 5-10° F. range.
Fig. 8(d) shows mean pressure distribution. Varying between 580 and 1,200 psi, the mean pressure is 827 psi and most data points are distributed in the 700-900 psi range.
The IGT-8 method or Equation 4 can determine distribution of dewpoint. Fig. 9a shows the dewpoints computed from the IGT-8 method by using daily averages of true temperature and pressure are very consistent with those calculated from using a sinusoidal model temperature and the overall average pressure. Their difference (SL residual) is very small, with a standard deviation of about 2.8 lb/MMscf.
The variation of SL residuals in Fig. 9a appears independent of time. Fig. 9b shows the SL residual following a normal distribution, applicable to all 28 lines investigated.
Fig. 9 suggests dewpoint can be well estimated by the sum of the deterministic SL (calculated from the sinusoidal model temperature, Equation 7, and the average pressure) and a corresponding SL residual (Equation 8).
For the 25 sets of field data that fit Category 1 and data sets that fit Category 2 sinusoidal models fit each data set and then resulting dewpoint residuals were statistically analyzed. The data of Categories 1 and 2, a total of 28 lines, represent more than 28 years of pipeline operation.
A bilinear regression model with the temperature average and amplitude as the independent variables can approximate the standard deviation of εϕs in Equation 8. Fitting the model to the data of the 28 lines yields Equation 9. The fixed value 0.5 in Equation 9 avoids the standard deviation going negative and maintains conservatism.
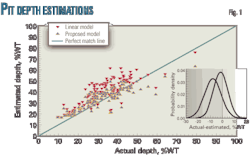
Fig. 10(a) shows the predictive capability of Equation 9, which shows the variation in standard deviation. The true standard deviation is determined for dewpoints predicted from Equation 4 using actual daily temperature and actual pressure. For a perfect model, all points would lie on the broken diagonal. Plotting the actual SL data and the 90% confidence bounds predicted with Equation 9 further verifies this predictability (Fig. 11).
Understanding the distribution of true dewpoints in Fig. 10(a) requires Fig. 10(b), in which 2-3 lb/MMscf is shown to have the most data points (10 points or 35.7% of total). The distribution is relatively similar in other ranges.
Although using Equation 9 is straightforward, it requires one additional step to make it practical. Using Equation 9 in its current state requires only two pieces of information from the operator: the mean operating temperature and the amplitude of seasonal variation in temperature.
Using Equations 4, 8, and 9 predicts dewpoint in an operating pipeline (Equation 10).
Fig. 11 shows the true dewpoints, determined from real operating temperature and pressure data, fall well within predicted 90% confidence bounds. Equation 10 predicts σSL in Fig. 11. Fig. 11(a) represents Category 1 data and Fig. 11(b) represents Category 2 data. Fig. 11(b) represents a worst case prediction due to the largest difference between the true standard deviation and that predicted from Equation 10. These two points appear as solid circles in Fig. 10(a).
The sinusoidal temperature data of the 28 lines, which serve as a basis for developing the model for prediction of dewpoints, can be presented as temperature amplitude vs. average temperature. These 28 data points appear in Fig. 8(a), in which all except three data points fall in the range of average temperatures between 50° and 100° F.
Equations 11 and 12 derive the two straight lines superimposed on Fig. 8(a).
Equation 11 represents the boundary of water freezing temperature, a temperature the operator seeks to avoid due to formation of ice in the presence of water. The upper-left cross-hatched region in Fig. 8(a) represents conditions under which the temperature could fall below water-freezing point.
Equation 12 is derived from Equation 10 when the two terms in the bracket are equal. The result is the lower-left line in Fig. 8(a). The cross-hatched region in the lower-left corner represents conditions in which the predicted standard deviation from the second term of Equation 10 is smaller than 0.5 but forced to be 0.5 in the model to avoid going below zero and maintain certain conservatism.
Field data of WC vs. time from more than 13 lines of four companies were collected and statistically analyzed. Fig. 12(a) shows variation of WC with time for 13 lines from three companies. Fluctuation of WC is more clearly seen for Companies A and B, while for Company C the fluctuation is relatively small. For Company B, two lines have WC exceeding 7 lb/MMscf.
Data from Company D are not shown in Fig. 12(a) because the data provided are either time independent or of short duration. The data from Company D do, however, have the advantage of representing a great number of lines or stations (at least 50).
Fig. 12(b) shows distributions of the statistical analysis of data received from all companies. The number of points for the WC interval below 3 lb/MMscf appears in light blue, between 3 (inclusive) and 5 in light grey, between 5 (inclusive) and 7 in purple, and 7 lb/MMscf and higher in green. The total number of points used for constructing the distribution for each line appears under the company symbols at the bottom of the chart. An overwhelming portion of WC is shown below 3 lb/MMscf.
Distributions of WC for all 13 lines from Companies A, B, and C and for Company D with many lines, allow building of empirical cumulative distribution functions for each set of pipeline data (Fig. 12(c)). Annual distribution of WC appears to vary widely between operators, and between lines of a given operator.
These distributions have shown vastly different values for both mean and variance, making it impossible to create a common distribution accurately capturing the variation seen in WC in each of these pipelines. Developing a worst-case distribution, however, represents a reasonable upper bound on the probability of water condensation in the pipelines. One possibility for this distribution is to use the largest values for the mean and variance from all of the pipelines. The red curve labeled WC in Fig. 12(c) is an example distribution, plotted as a lognormal distribution with a mean of 3.87, and a standard deviation of 1.80.
Fig. 12(d) shows the probability density function of the conservative lognormal distribution of the WC, in which WCs at 5, 7, and 3.87 (mean of the distribution) appear as the broken vertical lines. The WCs of 5 and 7 are typical TLs and will be used to develop operating charts.
Since operating temperature partially determines the likelihood of IC threat, understanding the variation of the time-averaged temperature with distance from a compressor station is helpful for evaluating how this variation of temperature affects IC threat along distance.
Fig. 13(a) shows field gas temperature of several lines. The temperature decreases in an exponential manner with distance from a compressor station. The law of energy conservation, that the loss of heat from gas equals the heat emission into ground, governs this exponential decay.
Data of temperature decay with distance, however, are insufficient to determine an IC threat without the seasonal amplitude. Knowing only seasonal amplitude data without knowing average temperature is likewise insufficient. Only one set of data shows the seasonal maximum and minimum temperatures vs. distance (Fig. 13(b)). This data set will later demonstrate the magnitude and variation of the likelihood of IC threat under conditions where the data are available.
References
1. Code of Federal Regulations (CFR), Title 49: Transportation, Part 192: Transportation of Natural and Other Gas by Pipeline Minimum Federal Safety Standards, Subpart O: Gas Transmission Pipeline Integrity Management:http://ecfr.gpoaccess.gov/cgi/t/text/text-idx?c=ecfr&tpl=/ecfrbrowse/Title49/49cfr192_main_02.tpl.
2. NACE, "Control of Internal Corrosion in Steel Pipelines and Piping Systems," NACE SP0106, 2006.
3. NACE STG 35, "Wet Gas Internal Corrosion Direct Assessment Methodology for Pipelines (WG-ICDA)," NACE draft standard in progress, 2010.
4. NACE, "Internal Corrosion Direct Assessment Methodology for Pipelines Carrying Normally Dry Natural Gas (DG-ICDA)," NACE SP 0206, 2006.
5. Bukacek, R.F., "Equilibrium Moisture Content of Natural Gases," Institute of Gas Technology Research Bulletin 8, November 1955.
6. NACE STG 31, "Prediction of Environmental Aggressiveness in Oilfield Systems from System Conditions," Draft Report, 2007.
7. Baldwin, R.M., "Black Powder in the Gas Industry - Sources, Characteristics and Treatment," Gas Machinery Research Council Report No. TA 97-4, 1988.
8. de Waard, C., and Lotz, U., "Prediction of CO2 Corrosion of Carbon Steel," NACE Corrosion 1993, New Orleans, Mar. 16-21, 1993.
9. Sridhar, N., Song, F.M., and Nored, M., "Guidelines/Quality Standards for Transportation of Gas Contaminating Mixed Corrosive Constituents," for PRCI, Contract GTI PF 00021435, PRCI ID: PR-015-03131, SwRI Project 18-06974, February 2004.
10. Mohitpour, M., Golshan, H., and Murray, A., "Pipeline Design and Construction: A Practical Approach," 3rd Edition, The American Society of Mechanical Engineers, New York, NY, 2007.
Based on presentation to ASME's International Pipeline Conference, Calgary, Sept. 27-Oct. 1, 2010.
The authors
Fengmei (Frank) Song ([email protected]) is a senior research engineer at Southwest Research Institute in San Antonio. He earned his PhD (2002) from the University of Toronto. He is a leading researcher in pipeline internal corrosion, external corrosion, and stress corrosion cracking, and their direct assessment methodologies. His work also involves evaluations of corrosion inhibitors and coatings and studies on microbiologically induced corrosion and corrosion fatigue. He is an active member of several technical committees of NACE International. He earned his BS (1989) and MS (1992) degrees from the China University of Petroleum.
John McFarland ([email protected]) is a research engineer at Southwest Research Institute, San Antonio. He also previously completed internships at Sandia National Laboratory and Los Alamos National Laboratory. He holds BS and PhD degrees in mechanical engineering from Vanderbilt University. He is a member of the Society for Experimental Mechanics.
Barron J. Bichon ([email protected]) is a research engineer at Southwest Research Institute in San Antonio. He holds a PhD (2010) from Vanderbilt University, an MS (2003) from University of Illinois at Urbana-Champaign, and a BS (2002) from the University of Memphis. He is a member of AIAA.
Luc Huyse ([email protected] ) is an inspection data modeler at Chevron Energy Technology Co. in Houston. He has also served as principal engineer at Southwest Research Institute in San Antonio and staff scientist at ICASE/NASA Langley Research Center in Hampton, Va. He is a past chair of the probabilistic methods committee of ASCE. He holds a PhD in structural reliability (civil engineering) from the University of Calgary. He is a member of ASME and NACE.
Fraser King ([email protected]) is president and principal consultant of Integrity Corrosion Consulting Ltd., Nanaimo, BC, and has been a researcher and consultant in the pipeline, petrochemical, and nuclear industries for the past 30 years. Fraser holds BS and PhD degrees from Imperial College of Science and Technology, London, and is a fellow of NACE International and a member of the Canadian Institute of Chemistry, the Electrochemical Society, the Materials Research Society, ASM International, and the American Nuclear Society.
Laurie Perry ([email protected]) is a team leader for the corrosion and direct-assessment group at Southern California Gas Co. in Los Angeles. She has served as a technical sales representative for Nalco Chemical Co. and a sales-service engineer for Flopetrol-Johnston-Schlumberger. She holds a BS in mechanical engineering from Pennsylvania State University and an MBA from Pepperdine University. She is currently vice-chair for the PRCI Corrosion Committee, and an active member of NACE and ASME.
Mark Piazza ([email protected]) is a senior program manager leading Pipeline Resource Council International's operations and integrity technical committee for pipeline programs. Prior to joining PRCI, he held positions with several corporations as an environmental manager directing the development and execution of compliance and remediation programs, with emphasis on restoration of impacted resources. His prior work included positions with PRCI members General Electric Co., Colonial Pipeline Co., and Total SA (through Atofina Chemicals). Piazza has served as a representative on trade groups and industry consortia, including the American Chemistry Council and the American Petroleum Institute. He is chair for the cathodic protection and corrosion control research and development technical exchange group of NACE. He holds a BS in geology and is a licensed professional geologist.
More Oil & Gas Journal Current Issue Articles
More Oil & Gas Journal Archives Issue Articles
View Oil and Gas Articles on PennEnergy.com