Digital twins predict hole cleaning

Digital twins are used in drilling for training simulators or visual aids. They have assisted upfront design studies and provided real-time interactive monitoring and control of automated drilling processes.

However, digital twins are only as good as their underlying physical models. Two studies were presented at the March 2020 IADC/SPE International Drilling Conference and Exhibition in Galveston, Tex., to perform real-time hole cleaning analysis with a focus on accurately calculating cuttings bed height. The developed models directly relate to torque and drag and equivalent circulation density, which are critical parameters to drilling.

Study 1

Researchers at the University of Texas developed a hole cleaning digital twin for predictive action. Hole cleaning is quantified using the following parameters:

• Total cuttings volume in the wellbore.
• Cuttings bed height.
• Cuttings concentration in suspension.
• Minimum annular velocity required to keep cuttings in suspension.
• Minimum annular velocity to move cuttings up-hole in an inclined wellbore.

Hole condition, in turn, is based on the following control variables:  

• Cuttings size.
• Drill pipe eccentricity.
• Mud weight.
• Mud rheology.
• Cuttings density.
• Hole size.
• Hole deviation.
• Flow rate.
• Rate of cuttings generation or rate of penetration (ROP).
• Drill pipe revolutions per minute (rpm).
• Hole cleaning pills or sweeps.

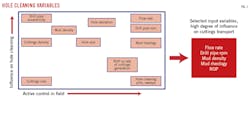
The most critical of these parameters for cuttings transport and hole cleaning are flow rate, rotary speed, mud properties (density and rheology), and weight on bit to control ROP (Fig. 1). These were selected as primary control in the digital twin.

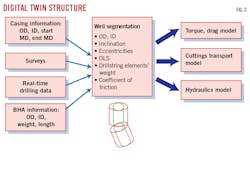
The digital twin incorporates real-time drilling data and analytical models with continuous crosschecking. Required real-time data include well profiles, bottom hole assembly (BHA) data (equipment weight, dimensions), casing information (diameters, set points), friction factors, and drilling parameters (rotational speed, weight on bit, etc.).

Calculated parameters include cuttings bed height, cuttings concentrations, equivalent circulation densities (ECD), and torque and drag calculated from industry-accepted analytical models. Analytical models were chosen because they run at high speed with good accuracy. Simulation speed is critical to evaluate multiple actions and sequences in real time. The digital twin structure is shown in Fig. 2.

Modeling

ECD is critical to manage downhole pressure, keeping it within the available drilling margin. At a given depth, ECD is determined by adding circulating friction pressure losses in the annulus and drillstring to the hydrostatic head. Frictional losses depend on wall roughness and friction, drillstring rpm, cuttings bed, annular restrictions, and drill pipe eccentricity.

The ECD model is adapted from the narrow-slot approximation based analytical hydraulics model for yield power law (YPL) fluids, modified to incorporate cuttings bed height and cuttings concentration in the flow. Temperature and drill pipe eccentricity are also included.

Torque and drag are modeled with analytical soft strings by segmenting the well into multiple intervals along the trajectory and considering effects of dog leg severity (DLS) between every two consecutive trajectory points. The model was tested and validated against data for 8.5-in. and 6.75-in. hole sections, and for various BHA configurations and casing setting points.

Cuttings modeling used a quasi-transient cuttings transport model which evaluates bed height based on the average inclination of a given well segment. Because wellbore inclination significantly affects cuttings transport efficiency, the well is divided into three distinct inclinations: 0-35°, 35-60°, and 60-90°.

Each inclination range has its own cuttings transport and bed height parameters. Hole cleaning in the 0-35° case primarily relies on viscosity and flow rate. In deviated and horizontal sections, drill pipe eccentricity and mud rheology force fluid to flow along the high side of the well resulting in flow velocity stratification from low velocity at bottom to high velocity at top. Therefore, drill pipe rotation is essential to lift cuttings into the flow stream on the high side of the hole.

The digital twin takes accumulated real-time data over 10-min intervals and segments the well into appropriate control volumes based on the latest information about its profile and trajectory. For every control-volume segment, calculations are made on critical transport fluid velocity (CTFV), critical re-suspension velocity (CRV), cuttings particle velocity, and average fluid flow velocity. These metrics calculate the height of the cuttings bed and concentration of cuttings in the flow stream in the different segments. Their evolution is tracked over time.

Bed height model testing and validation compared simulation results against data from extensive experimental work performed at the University of Tulsa. The difference between simulations and experiment averaged around 5% and remained within 10% for all cases. The cuttings transport model, in conjunction with the hydraulics model, was also implemented and tested on multiple wells.

Methodology

Hole cleaning is a stochastic sequential decision-making problem and can be solved using scenario analysis or RL methods by representing the system as a Markov reward process (MRP). To represent a system as an MRP, the following definitions are required:

• State of the system.
• Action space.
• Rewards associated with taking certain actions from certain states.
• The underlying models to evaluate the actions.
• Decision epoch or the time step for evaluation.
• Time horizon.

For the digital twin, state of the system is characterized by variables such as cuttings bed height, ECD relative to safe drilling margin, concentration of cuttings in the vertical section, and wellbore friction factor. Action space is a combination of discrete values of control parameters, such as discrete step changes in combinations of flow rate, drill pipe rotation speed, drilling speed or ROP, mud density, mud plastic viscosity (PV), and mud yield point (YP). The underlying models are as described above. Decision epoch is the time step for which decisions are made. In the case of this digital twin, the epoch is 10 min. Time horizon is time into the future for which the action sequence is to be decided.

The MRP system simulates multiple scenarios to find an optimal path to maximize long-term return. Such a system is referred to as a Markov decision process (MDP).

The method was applied to a well segment at 10,000-ft depth for illustration. The state of the system was represented by ECD, cuttings bed height, and cuttings concentration along the depth of the well. Five actions in 10-min. steps were simulated by varying ROP, rpm, and flow rate. Rewards were defined as reduction of the cuttings bed height, reduction of cuttings concentration in vertical section flow, and maintaining ECD within safe drilling margins. Certain actions reduced cuttings bed while keeping ECD within the drilling margin, while other actions reduced cuttings bed but simultaneously significantly increased ECD. Some actions left the system unchanged and were considered negative reward actions, since there was no improvement in the hole condition. The proven methodology was then applied to a case study.

Case study, results

Testing used an operator dataset of a well with casing running and cementing problems, probably caused by inefficient hole cleaning. The data included 1-sec interval real time surface drilling data, well surveys, mud check information, BHA-bit details, casing point information, and bit run summaries derived from daily morning reports.

The well had a short vertical section with kick off point around 500 ft. The landing point was around 1,300 ft after which it was laterally drilled to 2,434 ft TD. There were inclination changes with sizeable dog legs in the lateral section. Drilling the well involved a considerable amount of slide drilling (about 40%).

Intermediate 13.375-in. casing was set at 623 ft, and subsequently a 12.25-in. hole section was drilled to TD. The well had no issues while drilling but problems were encountered associated with poor hole cleaning while pulling out of hole (POOH) and running casing. During back-reaming operations, an increase in torque was logged at multiple depths and debris with excessive particle size and in large concentration was unloaded.

Resistance was encountered while running in the 9.625-in. casing, hitting a bridge around 1,650 ft. Finally, pulldowns were used to set casing in place. Slurry pumped during cementing resulted in intermittent losses and the casing string locked up and had to be pulled free.

To understand these issues the hole cleaning process was digitally twinned. The entire drilling operation for the well was simulated using 10-min time steps. Cuttings bed height, concentration of cuttings in flow, and ECD along the entire well were estimated at every evaluation interval. Simulations were performed for both drilling and circulation phases. Fig. 3 demonstrates the estimated height of the cuttings bed at the end of the drilling cycle (before starting the circulation phase) and the height of the cuttings bed after pulling the drillstring out of hole.

The cuttings bed after the well reaches TD was between 8.5 and 9.75 in. (in a 12.25-in. hole) along the depth of the well. After drilling, the well was circulated at 960 gpm with 80 rpm for about 60 min. After circulation, POOH intermittent back-reaming was carried out at 60 rpm with 950 gpm flow rate until the intermediate casing shoe was reached.

Based on this hole cleaning operation, the digital twin calculated a 4.75-in. cuttings bed after POOH, slightly under the 4.92-in. theoretical maximum allowed based on safe running of 9.625-in. casing in the given well profile. High cuttings beds in combination with potential micro-doglegs in the well trajectory and eccentricity of casing in lateral sections therefore likely caused the casing running problems.

Digital twin operation

The digital twin plans actions and realizes scenarios based on accurate interpretation of real-time data. To test it, multiple scenarios were generated starting from the state the well was in at the end of drilling operations (just after TD). Multiple options were generated by the digital twin for the 60-min circulation period during wellbore cleanup. Variables, shown in Table 1, included flow rate, drill pipe rpm, mud viscosity (PV, cp) and mud yield point (lbf/100 sq ft). The goal was to find the best scenario to reduce cuttings bed height. Fig. 4 shows results of eight simulations.

Action Set 0 contains parameters followed on the rig and resulted in a 6-in. bed height (dashed red line on graphs). If mud rheology is altered by increasing PV and reducing YP (Action Set 1), bed height reduces to about 4 in. If rheology is not altered, but only flowrate or rpm is increased (Action Set 2, Action Set 4) cuttings bed height will similarly reduce to about 4 in. If both RPM and flow rate increase without altering rheology (Action Set 6), cuttings bed height will reduce to under 2 in. and will reduce to under 1 in. with increased PV and decreased YP (Action Set 7). These eight actions help understand and quantify the effects of changes in different drilling parameters on the state of the system, providing real time guidance on the rig.

Study 2

Baker Hughes reported a method for a drilling fluid digital twin which connects geology, rheology, historical data, and drilling parameters to ultimately predict lateral cuttings bed height in real time. Additionally, downhole high-pressure high-temperature (HPHT) fluid properties are immediately available on site without the delay required for lab tests.

Cuttings bed development in highly inclined or horizontal intervals is primarily controlled by fluid rheology and mud flow rate to keep bed height low, minimizing torque and drag or avoiding stuck pipe. However, bed height is highly affected by pipe rotation and eccentricity. It is difficult to predict and impossible to monitor downhole. Computational fluid dynamic (CFD) simulations and machine learning were used to create an extensively parameterized model for fluid velocity above the bed, a critical parameter for hole cleaning. By using automated machine learning (autoML), the model can interpret real-time data from the drilling process.

Determining local velocity above the bed enables dynamic force calculations on settled cuttings on the bed, a critical parameter for particle motion and bed height predictions. Current empirical or mechanistic models do not effectively capture pipe eccentricity, rotation, inclination, and relative bed height development to pipe bottom.

Bed height predictions

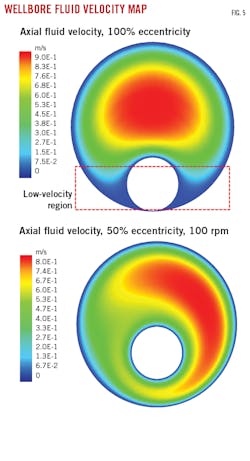
The work in this article takes the discussed parameters into account to create numerous two-dimensional CFD simulations to provide average fluid velocities above the cuttings bed. Fig. 5 shows an illustration of the 2D physical structure in the casing with velocity map for an eccentric pipe with and without rotation.

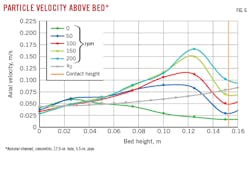
Fig. 6 shows an example from multiple simulations over a range of rpm and pipe concentricity. This case is for concentric pipe. The x-axis corresponds to cuttings bed height, the y-axis corresponds to average velocity at the center of a 5-mm particle above the bed.

Initially, when the cuttings bed is far from the drillstring wall (depicted by the “contact height” vertical line), rotational speed does not significantly affect average velocities, and CFD-derived velocities (vcfd) are similar to v0, the local average velocity estimate based on empirical work.

When the cuttings bed height reaches 0.06 m, average axial velocities become more sensitive to rotational speeds and vcfd begins to deviate from v0. The maximum deviation occurs at approximately 0.125 m. At higher bed depth, vcfd declines as the distance decreases between the cuttings bed surface and drillstring wall.

In concentric cases with no rotation, bed height increases from low-velocity regions between the cuttings bed and lower side of the drillstring. In an eccentric case, the low-velocity region exists without any cuttings bed and continues until the bed is high enough to cover the narrow regions and force fluid to flow through a wider region (Fig. 5, top). With drillstring rotation, high momentum diffusion in narrow regions is counteracted by advection of axial flow (Fig. 5, bottom). This counteraction results in higher average fluid velocities close to the cuttings beds at higher bed heights.

The results show that numerous factors affect bed height and must be considered, but CFD calculations are too complicated to perform in real time. Therefore, 54,586 records from CFD simulations were obtained from a matrix of typical values for drillstring and wellbore geometry, fluid density, flow rate, rotational speed, and additional parameters. These records trained an autoML algorithm for accuracy and real-time deployment.

Data were divided into a training set (90%) and a test set (10%). AutoML options were applied and the best model determined by coefficient of variation (CV) was an ensemble algorithm with 98% accuracy (Fig. 7).

After the model is trained, real-time analysis of cutting beds behavior can be performed on site to help guide drilling and drilling fluid decisions on the rig.

Rheology predictions

The digital twin approach also determined drilling fluid rheology vs. measured depth. Traditionally, rheology is measured at surface using rotational viscometers measuring shear stress at a given standard shear rate (viscometer rpm). This requires time to collect representative samples and presents uncertainty in translating surface results to downhole conditions. The digital twin takes surface measurements (at API standard conditions) and data from mud compositional analysis to estimate rheological properties in downhole conditions.

Herschel-Bulkley and YPL models described drilling fluid rheological behavior using 25 years of laboratory data randomly divided between a training set (85%) and test set (15%).

Applying autoML determined the most accurate model for each algorithm. Results were much like those shown in Fig. 7 for the bed height case, with the ensemble model achieving 96% accuracy.

References

1. Mayani, M.G., Svendsen, M., and Oedegaard, S.I., “Drilling Digital Twin Success Stories the last 10 Years,” SPE-191336-MS, SPE Norway One Day Seminar, Bergen, Norway, Apr. 18, 2018.
2. Saini, G.S., Ashok, P., and Oort, E., “Predictive action planning for hole cleaning optimization and stuck pipe prevention using digital twinning and reinforcement learning,” IADC/SPE-199548-MS, IADC/SPE International Drilling Conference and Exhibition, Galveston, Tex., Mar. 3-5, 2020.
3. Shirangi, M.G., Ettehadi, R., Aragall, R., Furlong, E., May, R., Dahl, T., Samnejad, M., and Thompson, C., “Digital Twins for Drilling Fluids: Advances and Opportunities,” IADC/SPE-199681-MS, IADC/SPE International Drilling Conference and Exhibition, Galveston, Tex., Mar. 3-5, 2020.

Based on presentations to the IADC/SPE International Drilling Conference and Exhibition, Galveston, Tex, March 3-5, 2020.